Лекция 11

Переходные процессы в линейных электрических цепях

Процессы, возникающие в ЭЦ при переходе от одного установившегося режима к другому называются переходными процессами ( или режимами). В переходных режимах ( в отличии от установившихся) токи и напряжения ветвей меняются непериодически.

Переход от одного установившегося режима к другому происходит мгновенно лишь в цепях, не содержащих накопителей энергии. Этот переход в цепях, содержащих индуктивные и емкостные элементы происходит за конечное время в связи с тем, что энергия электрического или магнитного поля, запасенная в соответствующем элементе при коммутации не может измениться скачком.

Возникновение переходных процессов связано с коммутациями в ЭЦ. В одних случаях переходные процессы являются нежелательными и опасными ( как, например, при коротких замыканиях в энергетических системах), в других- нормальными (естественными) режимами работы. Например, процессы, связанные с зарядом и разрядом конденсатора лежат в основе работы многих типов электронных генераторов.

В ряде случаев мгновенные значения токов и напряжений, возникающих в переходных режимах во много раз могут превысить их установившиеся значения. Отсюда видна актуальность задачи расчета и анализа переходных процессов в ЭЦ.

Расчет переходных процессов в ЭЦ во временной области.

Классический метод расчета переходных процессов.

Расчет переходных процессов в ЭЦ классическим методом сводится к составлению и решению дифференциального уравнения или системы дифференциальных уравнений ЭЦ. Эти уравнения составляются по законам Кирхгофа для контуров и узлов ЭЦ, сложившейся после коммутации, относительно мгновенных значений токов и напряжений. Если система уравнений полностью описывает рассматриваемую цепь, то последовательно исключая переменные , ее можно свести к одному дифференциальному уравнению вида

где Х - напряжение на емкостном элементе или ток в индуктивном элементе.

В качестве примера в табл. 1 приведены дифференциальные уравнения, описывающие переходные процессы , протекающие в схемах эл. цепей, представленных на рис. 11.1,а,б,в.

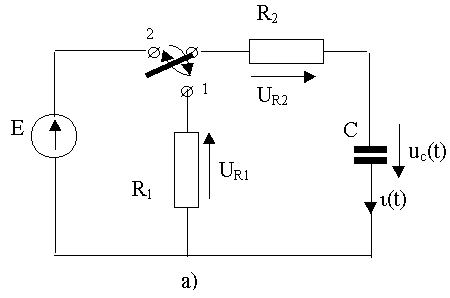
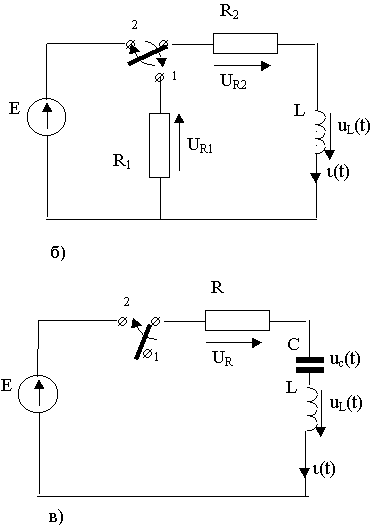
рис. 11.1,а,б,в

Каждой цепи, представленной на рис. 11.1,а,б, соответствует 2 уравнения. Одно из них описывает процессы, происходящие при перебросе ключа из положения "1" в положение "2" , второе -процессы при обратном перебросе.

Табл.1

Решение диф. уравнения может быть представлено в виде суммы принужденной X _пр и свободной X_св составляющей переходного процесса, т.е.

X(t)= X _пр +X_св.

Принужденная составляющая представляет собой частное решение уравнения (1) и определяет значение интересующей нас переменной в новом установившемся режиме. Этот режим называют принужденными, поскольку установившиеся токи и напряжения в этом режиме изменяются с той же частотой, что и действующие в цепи принуждающие ЭДС или токи. Так если в цепи имеются только источники постоянного напряжения или тока, то X_пр=Const. Если напряжения или токи источников меняются по синусоидальному закону ( f(t)=A_mSinw t), то принужденная составляющая представляет собой синусоидальную функцию времени той же частоты

X_пр = В_m Sin(w t+y ) .

Значения принужденных составляющих процессов для цепей, приведенных на рис.11.1, представлены в табл.2.

Следует заметить, что принужденные составляющие для цепей с источниками постоянного напряжения и тока могут быть найдены непосредственно из диф. уравнения , если все производные в нем приравнять нулю. Например, для цепи на рис.11.1,а при положении "2" ключа диф. уравнение имеет вид R₂Cdu_c/dt+u_c=E и, следовательно u_cпр=Е. Заметим также, что принужденные составляющие всех токов и напряжений могут быть найдены путем расчета установившегося режима в данной цепи и поэтому нет необходимости составлять диф. уравнение относительно каждой интересующей нас переменной.

Табл.2

Свободная составляющая процесса X_св определяется общим решением диф. уравнения (1). Физически эта составляющая определяет закон рассеяния энергии, первоначально запасенной в накопителях энергии ( индуктивных и (или) емкостных) в цепи свободной от источников энергии . Именно эта составляющая определяет характер и время переходного процесса.

В зависимости от порядка n диф. уравнения (1) различают ЭЦ первого, второго и высокого порядка. Сам порядок определяется числом ветвей с накопителями энергии. В цепях первого порядка накопление энергии происходит только в одном элементе (индуктивном или емкостном). Очевидно, что цепи, приведенные на рис.11,1,а и б являются цепями первого порядка. Одноконтурная цепь, содержащая 2 разнородных накопителя (индуктивный и емкостной), является цепью второго порядка (рис.1.11,в). Разветвленные цепи могут быть и более высокого порядка даже при наличии элементов только одного типа (L или C).

Характер свободной составляющей переходного процесса зависит от вида корней характеристического уравнения ЭЦ. В общем случае диф. уравнению (1) соответствует характеристическое уравнение

Характеристические уравнения и их корни для цепей, представленных на рис.11.1 приведены в табл. 3.

Табл.3

Если все корни характеристического уравнения вещественные и разные, то свободная составляющая отыскивается в виде суммы n экспоненциальных составляющих

,

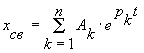где p_k - k-й корень характеристического уравнения, n - степень характеристического уравнения или порядок дифференциального уравнения.

Если корней характеристического уравнения имеются комплексно-сопряженные, то каждая пара таких корней p_{k, k+1}= -d ± jw _св , дает составляющую общего решения вида

,

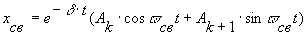представляющей колебательный процесс с периодом Т_св = 2p /w _св и экспоненциальной огибающей Ae^{- d t}.

Если среди вещественных корней уравнения имеются кратные p_k=p _k+1= -d , то составляющая общего решения, обусловленная этими корнями, имеет вид

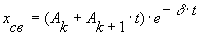
Свободные составляющие процессов для рассматриваемых цепей приведены в табл. 4.

Следует заметить, что свободный процесс происходит в цепи, освобожденной от источников энергии. При отсутствии источников свободные токи и напряжения должны со временем затухать. Следовательно, вещественные корни характеристических уравнений или вещественные части комплексно-сопряженных корней должны быть отрицательными.

Табл.4

Если характеристическое уравнение имеет степень n, то отысканию подлежат в общем случае n постоянных интегрирования A₁,A₂, ... A_n. Постоянные интегрирования находятся в результате решения системы из n уравнений, соответствующих моменту коммутации t=0, то есть

X(0) = X_пр(0)+ X_св(0)

X'(0) = X'_пр(0)+ X'_св(0)

X"(0) = X"_пр(0)+ X"_св(0)

------------------------------

------------------------------

X ^n-1(0) = X ^n-1_пр(0)+ X ^n-1_св(0)

Постоянные интегрирования определяются из начальных условий, т.е. условий в цепи в начальный момент времени после коммутации. Обычно полагают, что коммутация происходит мгновенно.

Энергия, запасенная в индуктивном и емкостном элементах в момент коммутации не может измениться скачком , т.е. сохраняет значение, имевшее место до коммутации и в момент коммутации и в первый момент после коммутации. Эти условия аналитически можно записать в виде

W_L(0_-)= W_L(0)= W_L(0₊)

и

W_С(0_-)= W_С(0)= W_С(0₊).

Поскольку энергия, запасенная в индуктивном элементе пропорциональна квадрату тока i _L, а энергия, запасенная в емкостном элементе - кавдрату напряжения u_C, то указанные выше условия можно привнести к виду

i _L (0_-)= i _L (0)= i _L (0₊), u_C (0_-)= u_C (0)= u_C (0₊).

Таким образом ток в индуктивном элементе и напряжение на емкостном элементе в момент коммутации не могут изменияться скачком. Эти утверждения носят название законов коммутации.

Ток в индуктивном элементе i _L (0_-) и напряжение на емкостном элементе u_C (0_-) непосредственно перед коммутацией называются независимыми начальными условиями.

Для определения начальных значений токов и напряжений можно воспользоваться схемой замещения, которая составляется из схемы цепи, сложившейся после коммутации, если заменить индуктивности идеальными источниками тока с токами ι_L(0), а емкости - идеальными источниками напряжения с ЭДС, равными u_C(0).

Значения постоянных интегрирования для рассматриваемых схем приведены в табл. 5.

Табл.5