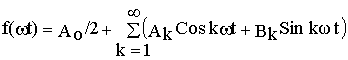
(10.1)
Лекция 10
Цепи несинусоидального периодического тока
Цепями периодического несинусоидального тока называются цепи токи в ветвях которых или напряжения на ветвях которых носят несинусоидальный периодический характер. Причинами возникновения в электрических цепях несинусоидальных периодических токов являются
1.Несовершенство (неидеальность) источников синусоидальных напряжений и токов.
2. Наличие в ветвях эл. цепей генераторов напряжений и токов специальной формы ( прямоугольной, пилообразной, трапециедальной и т.п.)
3. Наличие нелинейных элементов в ветвях эл. цепей.
1. Представление несинусоидальных напряжений и токов рядами Фурье
Из курса математики известно, что любую несинусоидальную периодическую функцию F(w t) удовлетворяющую условиям Дирихле, т.е. имеющую за полный период конечное число максимумов, минимумов и разрывов первого рода, можно представить в виде ряда Фурье
|
|
(10.1) |
где К=1, 2, 3….или представить в виде суммы бесконечного числа гармонических составляющих с частотами целыми и кратными основной частоте w . При этом все амплитудные коэффициенты ряда определяются формулами Эйлера -Фурье
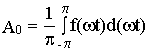 ;
; 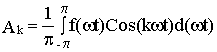 ;
;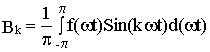 .
.
Для основных типов периодических функций, имеющих прямоугольную, треугольную, трапециевидную и др. формы, выражения для коэффициентов ряда Фурье приводятся в справочниках. Примеры разложений несинусоидальных периодических сигналов типовых форм приведены на рис.10.1.
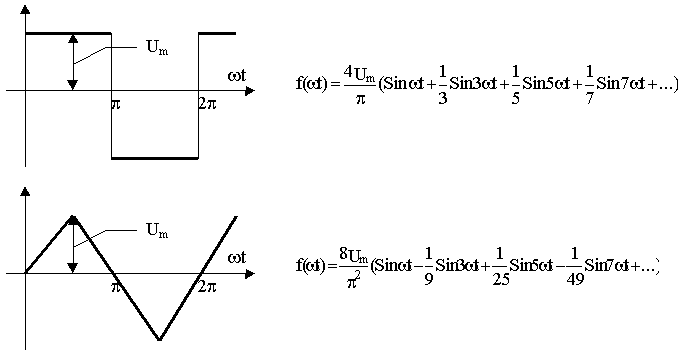
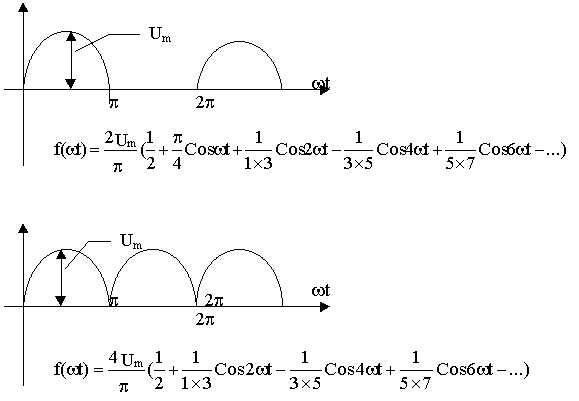
Рис. 10.1
В тех случаях, когда представить аналитически несинусоидальную функцию не представляется возможным или она задана в виде графика (или осциллограммы), амплитудные коэффициенты ряда можно получить графо-аналитически.
Этот метод основан на замене определенного интеграла суммой конечного числа слагаемых. Для этого период функции f(w t)=f(x) разбивается на n равных отрезков D X=2p /n, как показано на рис.10.2. и находятся значения функции f(x) в середине каждого интервала.
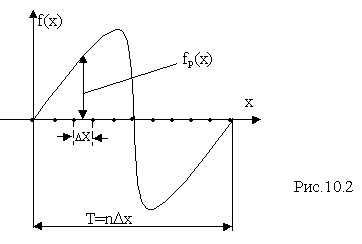
После этого вычисляют коэффициенты ряда по формулам
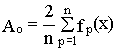 ;
; 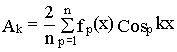 ;
; 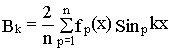 ,
,
где fp(x), Cospkx , Sinpkx -значение функции f(x), Cos kx и Sin kx в середине р-го интервала или
fp(x)= f(x)Ѕ x=(p-0.5)D x, Cospkx= CoskxЅ x=(p-0.5)D x, Sinpkx= SinkxЅ x=(p-0.5)D x.
После тривиальных преобразований ряд (10.1) можно переписать в виде
|
|
(10.2) |
где 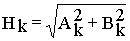 ,
, 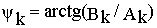 .
.
Таким образом после разложения аналитического или графо-аналитического периодические несинусоидальные ток и напряжение можно представить в виде
i= I0 + I1msin(w t +yi 1) + I2msin(2w t +yi 2) +ј + Irmsin(kw t +yi k))+ј , (10.3)
u= U0 + U1msin(w t +yu1) + U2msin(2w t +yu2) +ј + Ukmsin(kw t +yuk))+ ..10.4)
Первыe члены рядов (10.3) и (10.4) (I0, U0) называются постоянными составляющими или нулевыми гармоникми. Вторые члены I1msin(w t +yi 1) и U1msin(w t +yu1) имеют частоту равную частоте несинусоидальной периодической функции f(wt) и называются первыми или основными гармоническими составляющими (коротко - гармониками). Остальные члены ряда вида Aksin(kwt+y k) имеют частоты в целое число раз k больше частоты основной гармоники и называются высшими гармоническим составляющими или гармониками. Каждая высшая гармоника в отдельности именуется по номеру k , т.е. вторая гармоника, третья гармоника и т.д.
2. Мгновенные, средние и действующие значение несинусоидальных периодических величин.
Выражение (10.3) и (10.4) характеризуют мгновенные значения несинусоидальных тока и напряжения.
При несинусоидальных периодических токах и ЭДС в электрической цепи возможно ввести понятия действующих значений аналогично тому, как это было сделано для синусоидальных величин.
Действующее значение тока I определяется через мгновенные значения как
|
|
(10.5) |
Если представить периодический несинусоидальный ток в виде (10. 3 ) и подставить в (10.5), то после интегрирования получим
|
|
(10.6) |
Следовательно, действующее значение несинусоидального периодического тока равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений всех гармоник.
Проведя аналогичные выкладки, можно получить выражения для действующих значений ЭДС и падения напряжения в виде
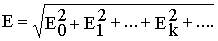 ,
,
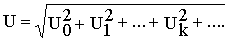 .
.
Средние за период значения несинусоидальных напряжений и токов определяются интегралом за период от соответствующего мгновенного значения и если последние представлены в виде соответственно ( 10. 3 ) и (10.4 ), то
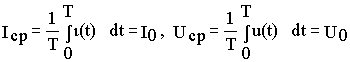 .
.
Как видно, средние за период значения несинусоидальных периодических величин равны их постоянным составляющим.
Средние по модулю или средние за положительный полупериод значения несинусоидальных напряжений и токов определяются интегралом за период от соответствующего мгновенного значения и если последние представлены в виде соответственно (10. 3 ) и (10.4 ), то
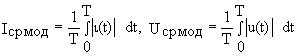 .
.
3. Оценка формы кривых несинусоидальных периодических величин
Как уже упоминалось выше, реальные источники электрической энергии в силу конструктивных особенностей формируют ЭДС и токи, отличающиеся от синусоидальных. Чаще всего эти величины симметричны, т.к. симметрична конструкция электромеханических генераторов, и не содержат четных гармоник.
Для оценки формы симметричных кривых используют коэффициенты формы kf , амплитуды kA и искажений kd.
Под коэффициентом формы kф понимают отношение действующего значения к среднему значению, взятому за положительную полуволну, т.е.
Kф = U/Uср мод.
Для синусоидальных величин kф » 1.11.
Под коэффициентом амплитуды kA понимают отношение амплитудного значения несинусоидальной величины к действующему, т.е.
kA = Um/U
(для синусоиды это значение равно 1.414)
Коэффициент искажений kи это отношение действующего значения основной гармоники к действующему значению несинусоидальной кривой, т.е.
kи = U1/U.
Поскольку идеальных синусоидальных величин практически не бывает, то в технике существует понятие практически синусоидальных кривых. Форма кривой считается практически синусоидальной, если все ее ординаты отличаются от ординат первой гармоники не более, чем на 5%. При этом количество контрольных точек должно быть не менее 12.
4. Мощность в цепях несинусоидального тока
Определим теперь среднюю мощность P в цепи при несинусоидальных токах и напряжениях. Она всегда может быть выражена в виде
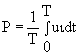
Подставляя в это выражение напряжение и ток, представленные выражениями (10. 3 ) и ( 10. 4 ), получим
|
P=U0I0+ U1I1Cos j 1+…+ UkIkCos j k+…, |
(10.7) |
где j k=yuk-yi k-фазовый сдвиг между к-ми гармониками напряжения и тока.
Из выражения (10.7) следует, что средняя или активная мощность в цепи с несинусоидальными токами и напряжениями равна сумме средних или активных мощностей отдельных гармоник.
По аналогии с цепями синусоидального тока можно ввести понятие полной или кажущейся мощности как произведение действующих значений тока и напряжения S = UI, тогда отношению P/(UI) можно придать смысл коэффициента мощности cosjэ.
Выражение нормально справедливо для некоторой электрической цепи синусоидального тока, в которой протекает ток с действующим значением I и существует падение напряжения U. При этом в цепи выделяется активная мощность P. Следовательно, при изучении некоторых явлений несинусоидальные токи и напряжения, не содержащие постоянных составляющих, можно заменить эквивалентными им по действующему значению синусоидальными со сдвигом фаз между ними jэ, соответствующим коэффициенту мощности несинусоидальных величин.
Для цепи несинусоидального тока реактивную мощность определить формально по аналогии с активной мощностью в виде
Q = U1I1sinj 1 + U2I2sinj 2 +ј + UkIksinj k + FACE="Symbol" SIZE=4>ј
Без доказательства отметим, что в цепях несинусоидального тока не существует связи между активной, реактивной и полной мощностью в виде треугольника мощностей, т.е.. 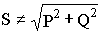
5. Расчет линейных ЭЦ с источниками периодических несинусоидальных напряжений и токов
Если все элементы электрической цепи с несинусоидальными токами и напряжениями линейны, т.е. параметры элементов не зависят от токов и падений напряжения, то анализ электромагнитных процессов в них можно проводить, используя разложение в ряды Фурье.
Расчет цепи при несинусоидальных токах проводится аналогично расчету при синусоидальных, но он должен выполняться отдельно для каждой гармоники, т.е. алгоритм расчета следующий:
-представить действующую в цепи ЭДС или ток рядом Фурье
-любыми методами расчета цепей синусоидального тока произвести расчет отдельно для каждой гармоники спектра;
-по полученному спектру искомых величин найти требуемые значения.
Пусть требуется найти активную мощность в цепи на рис.10.3 , где приложенное напряжение равно u(t)=10+20sin(1000t- 30° )+5sin(3000t+45° ) В, а параметры элементов R = 20 Ом, C = 50 мкФ и L = 5 мГн.
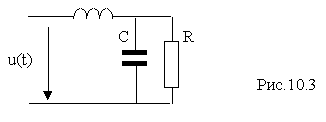
Спектр приложенного напряжения содержит постоянную составляющую или нулевую гармонику, а также первую и третью гармоники.
Реактивные сопротивления цепи зависят от частоты. Для k-й гармоники их можно представить через сопротивления на частоте основной гармоники в виде
XLk=kw 1L=kXL1; XCk=1/kw 1C=Xc1/k;
где xL1 = w 1L= 5 Ом и xC1 = 1/(w 1C) = 20 Ом - индуктивное и емкостное сопротивления на частоте основной гармоники. При расчете реактивных сопротивлений можно формально считать постоянную составляющую нулевой гармоникой. При этом xL0 = 0, а xC0 = µ , что соответствует отсутствию этих элементов и вполне согласуется с теорией цепей постоянного тока, где в статических режимах реактивных элементов нет.
Общее комплексное сопротивление цепи на частоте k-й гармоники будет
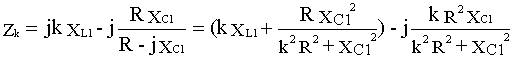
Подставляя в это выражение значения k = 0, 1, 3, получим значения общих комплексных сопротивлений на всех гармониках в виде Z0 = 20 Ом ; Z1 = 10- j5 Ом ; Z3 = 2+j9 Ом . Из этих выражений видно, что комплексные сопротивления на разных частотах могут иметь реактивную составляющую разного знака. Отсюда комплексные значения токов - I0 = U0/Z0 = 10/20 = 0.5 А;
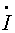 m1 =
m1 =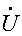 m1/Z1 = 20e- j30° /(10- j5) = 1.78e- j3.4° А;
m1/Z1 = 20e- j30° /(10- j5) = 1.78e- j3.4° А; 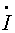 m3 = Um3/Z3 = 5e j45° /(2+j9) = 0.54e- j32.4° А.
m3 = Um3/Z3 = 5e j45° /(2+j9) = 0.54e- j32.4° А.
Полученные комплексные значения составляющих спектра токов можно представить рядом Фурье в виде
i = 0.5+1.78sin(1000t- 3.4° )+0.54sin(1000t- 32.4° ) А.
Теперь можно определить активную мощность в цепи как
P=U0I0+ U1I1Cos j 1+ U3I3Cos j 3=
10ґ 0.5+ (20ґ 1.78/2) ґ Cos[-30o –(-3.4o)]+ (5ґ 0.54/2) ґ Cos[45o –(-32.4o)]=22.2 Вт