Лекция1
Идеализированные элементы электрических цепей
Электротехническое устройство с происходящими в нем и в окружающем его пространстве физическими процессами в теории электрических цепей заменяется некоторым расчетным эквивалентом –электрической цепью (ЭЦ). Такая цепь состоит из идеализированных элементов активных и пассивных, которым теоретически приписываются определенные и магнитные свойства, так что процессы в электрической цепи приближенно отражают процессы в реальном устройстве, но могут быть проанализированы с использованием законов Ома и Кирхгофа.
Среди идеализированных элементов различают активные и пассивные элементы. К активным элементам относятся источники энергии (источники напряжения и источники тока). К пассивным элементам относятся резистивный элемент, индуктивный элемент и емкостной элемент.
Идеальный источник напряжения представляет собой элемент с двумя зажимами, напряжение на которых не зависит от сопротивления нагрузки ( или от тока нагрузки). Условное обозначение источника и его вольт-амперная характеристика представлены на рис.1.1, а,б сплошными линиями.
Стрелкой на рис. 1.1, а указано положительное направление ЭДС источника, т.е. направление возрастания потенциала в источнике. Идеальный источник напряжения представляет источник бесконечно большой мощности. Источник конечной мощности изображается в виде источника ЭДС с подключенным к нему последовательно элементом R, который ограничивает мощность, отдаваемую источником во внешнюю цепь
. Вольт-амперная характеристика источника конечной мощности показана на рис.1.1,б штриховой линией.Идеальный источник тока представляет собой элемент с двумя зажимами, ток во внешней цепи которого не зависит от сопротивления нагрузки ( или от напряжения на нагрузке). Условное обозначение источника и его вольт-амперная характеристика представлены на рис.1.2, а,б сплошными линиями.

Стрелкой на рис. 1.2, а указано направление перемещения положительных зарядов в источнике. Идеальный источник тока представляет источник бесконечно большой мощности. Источник конечной мощности изображается в виде идеального источника с подключенным к нему параллельно элементом R, который ограничивает мощность, отдаваемую источником во внешнюю цепь. Вольт-амперная характеристика источника конечной мощности показана на рис.1.2,б штриховой линией.
Резистивный элемент-идеализированный элемент ЭЦ, характеризующий потери энергии на нагрев, механическую работу или электромагнитное излучение в реальном электротехническом устройстве. Буквенное обозначение R используется как для обозначения самого резистивного элемента ( рис.1.3,а),
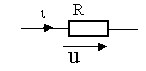
Рис. 1.3,а
так и для количественной оценки отношения напряжения на его зажимах к току, через него протекающему.
R(Ом)=u (В)/
i (А). (1.1)Эта формула выражает закон Ома, экспериментально установленный в 1826 году. Величина g=1/R называется проводимостью и измеряется в Сименсах..
Если вольт-амперная характеристика (ВАХ) резистивного элемента линейна (рис.1.3,б),
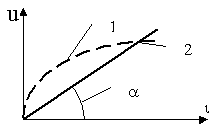
Рис. 1.3,б
то резистивный элемент называется линейным. Если задана ВАХ линейного резистивного элемента, то величина сопротивления его пропорционально тангенсу угла
a наклона ВАХ к оси токов, т.е.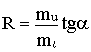 .
.
В силу пропорциональной зависимости (1.1) ток в линейном резистивном элементе всегда совпадает по форме с напряжением на его зажимах.
Для любого двухполюсника с мгновенным значением напряжения на его зажимах
u и мгновенным значением тока, протекающего через его зажимы i , мгновенная мощность p, характеризующая мгновенную скорость изменения энергии в элементе, определяется произведениемp=u
i (Вт).Мгновенная мощность может быть положительной либо отрицательной в зависимости от соотношения знаков напряжения и тока. Если p
> 0, то энергия поступает в элемент из внешней цепи. Если p< 0, то энергия запасенная в элементе возвращается во внешнюю цепь. Сама энергия W всегда положительна и определяется интегралом от мгновенной мощности.Для резистивного элемента мгновенная мощность всегда положительна и определяется как
р=u
i =u2/R=i 2R=u2g.Электрическая энергия, поступившая в резистивный элемент и превращенная в тепло, начиная с некоторого момента времени t=0 и до рассматриваемого момента t определяется интегралом
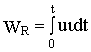 Дж.
Дж.
Превращение электрической энергии в тепловую впервые было доказано Джоулем и Ленцем опытным путем. Они установили тепловой эквивалент электрической энергии 0.24 кал/дж. Следовательно, количество тепла, эквивалентное рассеянной в резистивном элементе энергии , равно
Q=0.24 WR
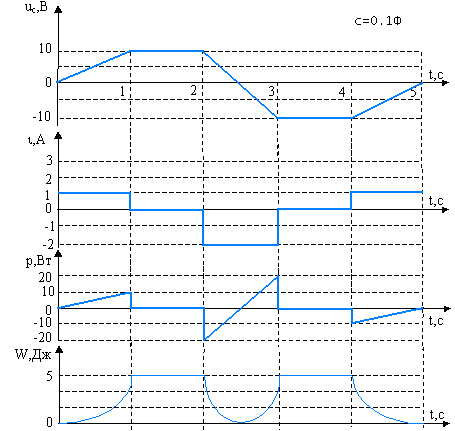
кал.Графики зависимостей
i (t), p(t) и WR(t) при произвольной форме напряжения на зажимах резистивного элемента представлены на рис. 1.3,в.
Рис. 1.3, в
Индуктивный элемент- идеализированный элемент ЭЦ, сходный по своим свойствам с катушкой индуктивности, способной запасать энергию магнитного поля. Он вводится в схему ЭЦ, если в реальном электро-техническом устройстве имеет место явление самоиндукции.
Условное обозначение индуктивного элемента приведено на рис. 1.4,а.
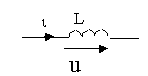
Рис. 1.4, а.
Буквенное обозначение
L применяется как для обозначения на схеме самого индуктивного элемента, так и для количественной оценки отношения потокосцепления самоиндукции y к току i , его обус-лавливающему. Это отношение называется индуктивностью элемента и измеряется в Генри. Таким образомL=
y /i (Гн).Физически картина состоит в следующем. Переменный во времени ток
i, протекая по виткам w катушки создает переменный магнитный поток Ф. Этот поток, пронизывая витки катушки, образует потокосцепление самоиндукцииy
=Фw.Всякое изменение потокосцепления самоиндукции во времени на основании закона электромагнитной индукции Фарадея -Максвелла обуславливает ЭДС самоиндукции
eL=- d
y /dtПо закону Ленца, выражающему принцип электромагнитной инерции, эта ЭДС препятствует изменению потокосцепления. Это обстоятельство учитывается знаком (-) в приведенной формуле. Величина по знаку противоположная ЭДС носит название напряжения на индуктивности u
L. Таким образомuL=- eL=d
y /dt.Если магнитный поток катушки формируется в ферромагнитной среде, то зависимость потокосцепления самоиндукции от тока
Y (i ) в общем случае нелинейна (кривая 1 на рис. 1.4,б) и, следовательно, индуктивность катушки зависит от тока, через нее протекающего.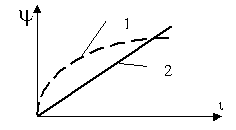
Рис. 1.4, б
Это обстоятельство связано с непостоянством магнитной проницаемости ферромагнитного сердечника. Если сердечник неферромагнитный, то магнитная проницаемость его постоянна. В этом случае зависимость
Y (i) линейна и индуктивность L является постоянной величиной.Для линейного индуктивного элемента напряжение на зажимах u
L связано с током следующей зависимостьюuL=- eL=d
y /dt=d(Li )/dt=L di /dt,т.е. напряжение на индуктивном элементе пропорционально скорости изменения тока, через него протекающего.
Если
i =I=Const, то uL=0, и следовательно индуктивный элемент в цепи с источниками постоянного напряжения и тока в установившемся режиме можно заменить проводником с нулевым сопротивлением.Если ток изменяется линейно (
i =At), то напряжение на индуктивном элементе постоянно (uL=LA).Если известно напряжение на индуктивном элементе, то ток через него определяется интегралом
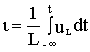 ,
,
где нижний предел принят равным -
Ґ в предположении, что до рассматриваемого момента времени процесс мог длиться сколь угодно долго. При t=0 имеем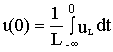 ,
,
и следовательно,
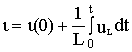 .
.
Мгновенная мощность
pL=uL
i =Li di /dtдля индуктивного элемента может быть и положительной и отрицательной , что зависит от знаков тока и производной тока. Если p>0, то энергия поступает из внешней цепи и запасается в индуктивном элементе. Если p<0, то энергия, запасенная в индуктивном элементе возвращается во внешнюю цепь. Сама энергия всегда положительна и определяется выражением
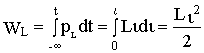 .
.
Как видно, в любой момент времени энергия пропорциональна индуктивности и квадрату тока, протекающего через индуктивный элемент. Графики зависимостей u
L(t), p(t) и WL(t) при произвольной форме тока i L(t) через индуктивный элемент представлены на рис. 1.4,в.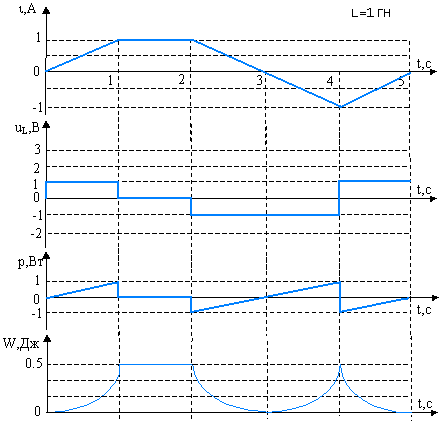
Рис. 1.4, в
Емкостной элемент- идеализированный элемент ЭЦ, сходный по своим свойствам с конденсатором, способным запасать энергию электрического поля.
Условное обозначение емкостного элемента приведено на рис. 1.5,а.
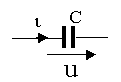
Рис. 1.5, а.
Буквенное обозначение С применяется как для обозначения на схеме самого емкостного элемента, так и для количественной оценки отношения заряда
q к напряжению на конденсаторе uc Это отношение называется емкостью элемента и измеряется в Фарадах. Таким образомС (Ф)=q(к)/u
c (В).Зависимость q(u
c) в общем случае нелинейна (кривая 1 на рис. 1.5,б) и, следовательно, емкость конденсатора зависит от от напряжения на его обкладках.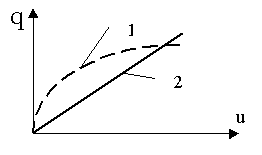
Рис. 1.5, б
Если зависимость q(u
c) линейна, то емкость С является постоянной величиной и говорят о линейном емкостном элементе.Для линейного емкостного элемента ток связан с напряжением u
c следующей зависимостьюi
=dq/dt=d(C uc)/dt=C duc /dt,т.е. ток через емкостной элемент пропорционален скорости изменения напряжение на нем. Если du
c /dt> 0, то ток положителен. Если duc /dt< 0, то ток отрицателен.Если u
c =U =Const, то i =0, и следовательно, в цепи с источниками постоянного напряжения и тока в установившемся режиме ветвь с емкостным элементом можно исключить (разорвать).Если напряжение изменяется линейно (u
c=At), то ток в емкостном элементе постоянен (i =СA).Если известен ток емкостного элемента , то напряжение на нем определяется интегралом
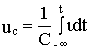 ,
,
где нижний предел принят равным -
Ґ в предположении, что до рассматриваемого момента времени процесс мог длиться сколь угодно долго. При t=0 имеем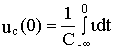 ,
,
и следовательно,
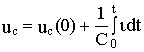 .
.
Мгновенная мощность
рс
=uсi =Сuсduс/dtдля емкостного элемента может быть и положительной и отрицательной , что зависит от знаков напряжения и производной напряжения . Если p>0, то энергия поступает из внешней цепи и запасается в емкостном элементе. Если p<0, то энергия, запасенная в емкостном элементе возвращается во внешнюю цепь. Сама энергия всегда положительна и определяется выражением
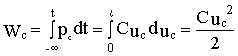 .
.
Как видно, в любой момент времени энергия пропорциональна емкости элемента и квадрату напряжения на его зажимах. Графики зависимостей
i(t), p(t) и Wc(t) при произвольной форме uс(t) представлены на рис. 1.5,в.