1. ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ. ЕЕ ПРЕОБРАЗОВАНИЕ

У Санкт-Петербургский государственный институт точной механики и оптики (технический университет), 2002

г Ю.М. Осипов, Е.А. Петров, 2002

Анализ разветвленных цепей постоянного и

переменного тока

СОДЕРЖАНИЕ

1. Электрическая цепь. Ее преобразование и определение входных сопротивлений

2. Законы Кирхгофа. Составление системы уравнений по схеме и графу цепи

3. Расчет разветвленных электрических цепей постоянного тока. Прямая и обратная задачи

4. Расчет цепей синусоидального тока символическим методом

5. Решение системы линейных уравнений на ПЭВМ

6. Приложение

7. Список литературы

В пособии изложена методика анализа линейных электрических цепей постоянного и переменного тока.

На примерах показано применение к расчету законов Ома и Кирхгофа.

Приведена последовательность использования ЭВМ при решении системы линейных уравнений с действительными и комплексными коэффициентами.

Приложение пособия содержит пять задач по двадцать пять вариантов каждая. Задачи могут быть использованы для аудиторных занятий и в качестве домашних заданий.

Пособие предназначено для студентов следующих направлений подготовки: 654000, 651100, 553100, 654400, 651900, 654300, 652300, 654500, 653700, 654600, 652000, 551900.

Рекомендовано кафедрой электротехники и прецизионных электромеханических систем СПбГИТМО, протокол № 3 от 29 декабря 2000 г.

ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ. ЕЕ ПРЕОБРАЗОВАНИЕ И ОПРЕДЕЛЕНИЕ ВХОДНЫХ СОПРОТИВЛЕНИЙ

Электрическая цепь содержит источники и приемники электрической энергии связанные проводами, что обеспечивает протекание токов по ее элементам.

Различают два типа источников: источники напряжения или ЭДС e, E и источники тока j, J. Идеализированный источник напряжения поддерживает неизменным значение напряжения на своих зажимах независимо от тока отдаваемого им в нагрузку. Его внутреннее сопротивление r равно нулю. Идеализированный источник тока обеспечивает постоянное значение тока, отдаваемого им в нагрузку независимо от напряжения на его зажимах. Внутреннее сопротивление этого источника r бесконечно велико.

Пассивными элементами электрической цепи являются: резистивный r, R, индуктивный L и емкостной C.

Рис. 1.1. Элементы электрических цепей

На рис. 1.1 показаны обозначения элементов на электрических схемах и условные положительные направления токов и напряжений. Перед анализом цепи необходимо указать эти направления; их выбор произволен.

Последовательное соединение элементов

Соединение двух и более элементов называется последовательным, если элементы связаны между собой простыми узлами. В таком узле ток не делится на части. Поэтому ток во всех элементах этого соединения остается неизменным.

На рис. 1.2,a показано последовательное соединение n резистивных элементов. Этот набор элементов можно заменить одним эквивалентным, вычисленным по формуле

Рис. 1.2. Эквивалентное преобразование последовательного соединения

элементов

Для последовательного соединения индуктивных и емкостных элементов используются аналогичные соотношения (рис. 1.2,б и рис. 1.2,в):

При объединении последовательно соединенных источников напряжений на рис. 1.2,г их суммируют алгебраически:

Последовательное соединение источников тока не рассматривается.

Параллельное соединение элементов

Соединение нескольких элементов называется параллельным, если их выводы объединены в два узла; на каждом элементе цепи имеет место одно и то же напряжение.

Узлом называют соединение трех и более элементов или ветвей. В узле ток разветвляется.

Рис. 1.3. Эквивалентное преобразование параллельного соединения элементов

На рис. 1.3,a показано параллельное соединение резистивных элементов. Его можно заменить эквивалентным, используя одну из формул:

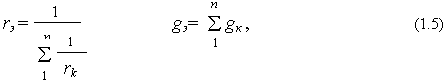
где g_k= 1/r_k; g _э= 1/r_э– проводимости элементов.

Для параллельного соединения элементов r₁ и r₂ имеем

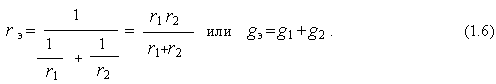
Для параллельного соединения индуктивных элементов, емкостных элементов и источников тока на рис. 1.3,б,в,г формулы имеют вид

в последнем соотношении токи суммируются алгебраически.

Параллельное соединение источников напряжения не рассматривается.

В разветвленных электрических цепях можно выделить фрагменты последовательно и параллельно соединенных элементов. Такое соединение называется смешанным. Постепенно, шаг за шагом, заменой отдельных групп элементов на эквивалентные, можно представить все элементы одним эквивалентным, присоединенным к источнику питания. Если такое преобразование осуществляется с резистивными элементами, то конечный результат называется входным сопротивлением цепи со стороны источника питания.

1.1.Определить входное сопротивление для схемы рис. 1.4 со стороны источника питания с напряжением u.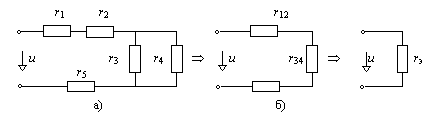

Рис. 1.4. Последовательность упрощения разветвленной цепи

Решение рекомендуем начинать с упрощения удаленных от источника питания элементов. На первом этапе объединяем последовательно соединенные элементы r₁ и r₂ и параллельно соединенные r₃и r₄ :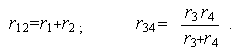

Схема упрощается и на рис. 1.4,б принимает вид последовательного соединения трёх элементов. На втором этапе суммируем r₁₂, r₃₄ и r₅ (рис. 1.4,в):

r_э= r₁₂+ r₃₄+ r₅.

В результате вся совокупность резистивных элементов сведена к одному эквивалентному, которое и будет входным сопротивлением цепи.

Задача решена.

1.2. Определить входные сопротивления для схем рис. 1.5.

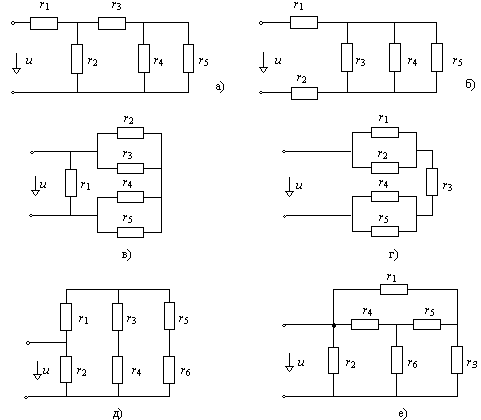
Рис. 1.5

Анализ этих схем показывает, что на рис. 1.5,a-д можно выделить последовательно и параллельно соединенные элементы, но в схеме рис. 1.5,е их нет. Чтобы получить такие группы элементов и на этой схеме, необходимо найти соединение "звездой" или "треугольником" и эквивалентно преобразовать одного в другое.

На рис. 1.6 показаны такие соединения и формулы эквивалентного

перехода.

Рис. 1.6. Преобразование ”Треугольник”Ы ”Звезда”

Варианты упрощения схемы на рис. 1.5,е могут быть следующими.

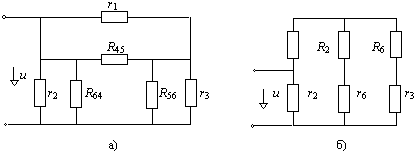
Рис. 1.7

Так преобразуя "звезду" r_4, r_5, r₆ в "треугольник", получаем схему рис. 1.7,a, где можно выделить параллельно и последовательно соединенные элементы. Аналогично можно, к примеру, преобразовать "треугольник" r_1, r_4, r_5, в "звезду" и также упростить схему (рис. 1.7,б). Возможны и другие преобразования.

1.3. Полагая все значения сопротивлений исходной цепи (рис. 1.5,е) равными 1[Ом], найти ее входное сопротивление, используя схемы на рис. 1.7.

1.4. Заменив в схемах рис. 1.5 все резистивные элементы на индуктивные и, сохранив прежнюю нумерацию элементов, определить эквивалентную индуктивность каждой схемы.

1.5. Заменить в схемах рис. 1.5 все резистивные элементы на емкостные с прежней нумерацией. Определить эквивалентную емкость цепи для каждой схемы.

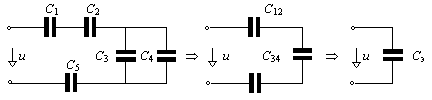
Рис. 1.8. Последовательность эквивалентного преобразования цепи

с емкостными элементами

Например, для схемы рис. 1.4 после такой замены получим рис. 1.8,а. Объединяя элементы по аналогичным формулам, найдем на первом этапе преобразования (рис.1.8,б)

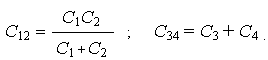
На втором этапе соответственно получим (рис. 1.8,в):

Задача решена.

Рассмотрены простейшие приемы преобразования пассивных цепей, составленных элементами R, L, C. Эквивалентные индуктивность, емкость и входное сопротивление определялись по отношению к выводам источника питания.

Однако существует необходимость в определении входного сопротивления относительно любой ветви пассивной цепи, получающейся после того, как напряжения источников ЭДС и токи источников тока исходной цепи приняты равными нулю. Например, при расчете тока в ветви методом эквивалентного генератора, при оценке результатов измерения напряжения вольтметром с малым внутренним сопротивлением.

Для определения входного сопротивления в данном случае необходимо выполнить следующее.

1. Разомкнуть ветвь, по отношению к которой требуется определить входное сопротивление. Зажимы разомкнутой ветви как-либо обозначить.

2. Исключить источники энергии, сохранив их внутренние сопротивления: источники напряжения закоротить (r_u= 0), а источники тока разомкнуть (r_j® Ґ ).

3. Объединяя последовательно и параллельно соединенные элементы, привести цепь к одному сопротивлению по отношению к обозначенным зажимам. Это сопротивление и будет входным со стороны рассматриваемой ветви.

1.6. Для схемы на рис. 1.9 найти входное сопротивление по отношению к пятой ветви.

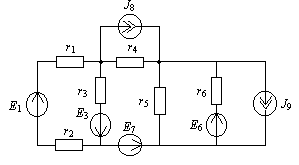
Рис. 1.9

На рис. 1.10,a показана схема цепи после исключения всех источников и сохранения их внутренних сопротивлений. В разомкнутой пятой ветви зажимы помечены символами m, n и показано стрелкой, что входное сопротивление R_вх5 определяется относительно именно этих зажимов.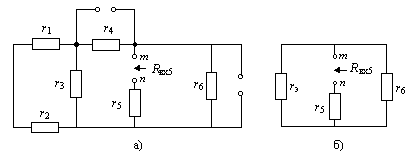

Рис. 1.10

На первом этапе объединяем элементы слева от пятой ветви

схема упрощается до представленной на рис. 1.10,б. Окончательно объединяем параллельно соединенные сопротивления r_э и r₆ и добавляем к ним сопротивление пятой ветви r₅:

Полученный результат и будет решением поставленной задачи.

1.7. Для схемы рис. 1.9 определить входные сопротивления со стороны ветвей: первой, третьей, четвертой, шестой и седьмой.

В следующих разделах пособия электрическая цепь относительно двух любых ее выводов будет рассматриваться как двухполюсник. Двухполюсник, содержащий источники энергии, будет называться активным. В пассивном двухполюснике источников энергии нет.

Изучение материала первого раздела пособия рекомендуем закончить решением первой и второй задач приложения. Вариант выбирайте самостоятельно или по рекомендации преподавателя.

2. ЗАКОНЫ КИРХГОФА. СОСТАВЛЕНИЕ СИСТЕМЫ УРАВНЕНИЙ ПО СХЕМЕ И ПО ГРАФУ ЦЕПИ

Независимо от формы и мощности сигналов, генерируемых источниками питания e(t) и j(t), токи и напряжения в любой электрической цепи подчиняются законам Кирхгофа. Полагаем: цепь, кроме источников содержит лишь резистивные элементы r.

Первый закон Кирхгофа – алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю

Положительные направления токов каждой ветви произвольны. Токи направленные к узлу принимаются отрицательными, направленные от него – положительными (или наоборот).

Второй закон Кирхгофа – алгебраическая сумма ЭДС в любом замкнутом контуре равна алгебраической сумме падений напряжений в нем.

Направление обхода контура произвольно. При записи левой части равенства те ЭДС, направления которых совпадают с направлением обхода контура принимаются положительными; ЭДС, направленные против выбранного направления обхода – отрицательными. При записи правой части равенства со знаком плюс берутся падения напряжения на тех элементах r_k через которые протекают токи i_k, положительное направление которых совпадает c направлением обхода и со знаком минус – падения напряжения на тех элементах, через которые протекают токи, положительное направление которых противоположно направлению обхода.

Cложная цепь содержит N_вветвей, объединенных в N_уузлов и N_J ветвей с источниками тока. В ней кроме резистивных элементов могут быть только источники тока, только источники ЭДС, источники ЭДС и тока совместно.

Порядок анализа на основании законов Кирхгофа

Определить число неизвестных токов, равное N_B - N_J.

Указать положительное направление тока в каждой ветви.

Составить N₁= N_у - 1 независимых уравнений по первому закону Кирхгофа.

Составить N₂=N_В- N_J- (N_У- 1) независимых уравнений по второму закону Кирхгофа. При составлении уравнений по второму закону Кирхгофа следует выбирать лишь те контуры, которые не содержат ветвей с источниками тока. Указать направление обхода контуров.

Число уравнений равно числу неизвестных токов N₁+ N₂= N_В- N_J.

2.1. Составить систему уравнений для цепи, схема которой изображена на рис. 2.1,а

Рис. 2.1

Цепь образована шестью ветвями ® N_B= 6, последняя содержит источник тока® N_J= 1. Нумеруем токи i₁ ё i₆и указываем произвольно положительные направления первых пяти (рис. 2.1,б). Последним током i₆полагаем ток источника i₆= j₆; их направления одинаковы.

В цепи четыре узла ® N_у= 4, указываем их номера на схеме. По первому закону Кирхгофа составляем три уравнения для трех узлов из четырех ® N₁= N_у- 1 = 4 - 1.

По второму закону Кирхгофа составляем два уравнения для контуров k и m не содержащих ветвь с источником тока

N₂= N_В- N_J - (N_У- 1) = 6 - 1 - (4 - 1) = 2.

Перед записью уравнений указываем направление обхода этих контуров (рис. 2.1,б).

узел 1	- i₂+i₅ - i₆= 0,
узел 2	i₁+i₄ - i₅= 0,
узел 3	- i₃- i₄+ i₆= 0,	(2.3)
контур k	r₁ i₁+ 0 i₂+ r₅ i₅= e₁+ e₂,
контур m	r₁ i₁+ r₃ i₃- r₄ i₄= e₁- e₄.

Решение данной системы уравнений показано в 3.1 при расчете цепи постоянного тока.

Составление системы уравнений по графу цепи

При анализе сложных цепей во избежание ошибок имеет смысл формализовать порядок составления уравнений Кирхгофа, выполняя его не по схеме цепи, а по ее упрощенному аналогу – топологическому графу.

Прежде уточним понятие ветви. Ветвью называют набор последовательно соединенных источников и приемников электрической энергии, имеющий два зажима для присоединения к другим участкам цепи. В качестве приемников рассматриваем лишь элементы r. Таким образом ветвь удобно рассматривать в виде обобщенного элемента цепи.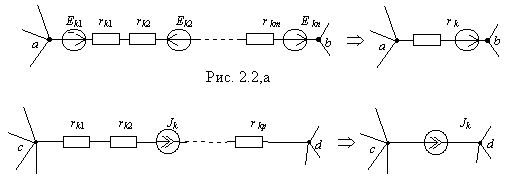

Рис. 2.2,б

Различают ветви с источниками напряжения – тип 1 и ветви с источниками тока – тип 2. Ветвь первого типа на рис. 2.2,a содержит в общем случае m сопротивлений и n источников напряжений. Используя формулы (1.1) – (1.4), можно объединить элементы и перейти к канонической схеме, содержащей минимум элементов и представленной справа на рис. 2.2,а, где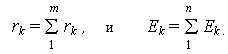

Ветвь второго типа не содержит несколько источников тока, что отмечалось ранее, но может включать набор сопротивлений (рис. 2.2,б). Используя формулу (1.1), целесообразно перейти к канонической схеме, где

Очевидно, что сопротивление ветви второго типа определяется только бесконечно большим сопротивлением источника тока J_k, сопротивление других ветвей не изменяет значение тока в ней. Следовательно, каноническая ветвь данного типа содержит только один источник тока. Переход от реальной схемы электрической цепи к эквивалентной, где каждая ветвь заменена на каноническую, не изменяет значений токов в ветвях и напряжений между узлами.

Обратимся к законам электрической цепи в общей формулировке.

Первый закон Кирхгофа: алгебраическая сумма токов в ветвях, сходящихся в любом узле, или сечении равна нулю –

Под сечением понимают любую замкнутую поверхность, рассекающую схему электрической цепи на две части: внешнюю по отношению к поверхности и внутреннюю. Его изображают в виде следа замкнутой поверхности, охватывающей часть схемы, включающей один или несколько узлов. Сечение обобщает понятие узла.

Второй закон Кирхгофа: алгебраическая сумма напряжений для любого замкнутого контура равна нулю –

Уравнения равновесия цепи, определяемые формулами (2.4) и (2.5), являются тождественными равенствами, справедливыми для любого момента времени.

Число и вид уравнений, которые следует составить для полного описания физических процессов в цепи, в первую очередь для определения токов и напряжений, зависят от способа соединения ветвей цепи и от их типа. Структуру цепи, определяемую способом соединения ветвей, будем анализировать, абстрагируясь от содержания каждой ветви: вместо схемы цепи исследуют ее топологический граф. При изображении ветвей графа целесообразно различать, какой тип ветви она заменяет. В пособии принято первый тип ветви изображать ветвью графа в виде сплошной линии (прямой или кривой), а для ветви второго типа, в которой значение тока определяется самим источником тока, в виде пунктирной линии. Ветви графа N_В и узлы N_У нумеруют в соответствии с номeрами ветвей схемы и узлов исходной цепи. Ориентация ветвей графа также должна соответствовать выбранным направлениям токов и напряжений исходной цепи. Так для канонической ветви первого типа (рис. 2.2,а) ток и напряжение выбираются всегда совпадающими по направлению, соответственно с этим направлением ориентируется и ветвь графа. Если эта ветвь содержит только источник напряжения, то она называется вырожденной и ее ориентация в графе производится по напряжению источника и направляется против действия ЭДС. Для ветви второго типа ветвь графа ориентируется по направлению действия источника тока.

Анализ топологического графа начинается выделением ветвей дерева графа N_Д и ветвей связи N_С. Ветви дерева образуют связный подграф, объединяющий все узлы, но не создают ни одного замкнутого контура. Выбор ветвей дерева произволен, но в него не включаются ветви графа, замещающие источники тока.

Ветви связи являются дополнением к ветвям дерева. Присоединение очередной ветви связи к ветвям дерева образует замкнутый контур, который называется главным контуром. В дальнейшем ветви дерева отмечаем на графе двойной линией, ветви связи – одинарной.

Число независимых уравнений N₁, составленных по первому закону Кирхгофа, соответствует числу ветвей дерева N_Д, т.е. определяется числом узлов без единицы:

N₁= N_Д= N_У- 1.

(2.6)

Последний по номеру узел считается зависимым узлом, для него уравнение по первому закону Кирхгофа не составляется и в систему уравнений не включается. Правило знаков для токов в уравнениях (2.4), произвольно; будем полагать токи, приходящие в узел отрицательными, а выходящие из него – положительными.

Число уравнений N₂, которые следует добавить по второму закону Кирхгофа, определяется соотношением

N₂= N_Н- N_Д= (N_B- N_J) - N₁= N_B- N_J - N_У+ 1

(2.7)

где N _Н =(N _В - N_J) – число ветвей с неизвестными токами, N_J – число ветвей с известными источниками тока. Уравнения равновесия записываются для системы главных контуров. Каждый главный контур образуется присоединением очередной ветви связи к ветвям дерева. Правило обхода контура согласуется с направлением ветви связи, входящей в контур. В систему главных контуров не включают ветви, замещающие источники тока.

К системе, состоящей из N_Н= (N₁+ N₂) добавляются уравнения, связывающие ток и напряжение в каждой отдельной ветви. Такие уравнения называются компонентными уравнениями, о них речь пойдет в следующем параграфе.

Изложенная методика позволяет составить правильную совместную систему уравнений для анализа цепей любой сложности.

2.2. Составить уравнения равновесия цепи (схема на рис. 2.3,a).

Рис. 2.3

Исследуемая цепь включает шесть ветвей (N_B= 6), из них две ветви содержат источники тока J₃ и J₆ (N_J= 2). На топологическом графе эти ветви изображены пунктирными линиями (рис. 2.3,б), их ориентация совпадает с направлением тока в ветви. Остальные ветви цепи относятся к ветвям первого типа, на графе они представлены сплошными линиями-ветвями 1, 2, 4 и 5. Для ветвей 1, 4 и 5 ориентация ветвей графа выбирается произвольной и согласуется с условным положительным направлением токов и напряжений для соответствующих ветвей схемы. Вторая ветвь является вырожденной, содержащей только источник ЭДС E₂, ориентация этой ветви графа согласуется с направлением напряжения этого источника – против действия его ЭДС. Выбрав в качестве ветвей "дерева" графа ветви 1,2 и 5 (N_Д= 3) и выделив их двойными линиями, завершаем построение графа цепи. Узлы обозначаем: 1, 2, 3 и 4; их на единицу больше числа ветвей "дерева": (N_У= 4).

В соответствии с ранее изложенным, окончательно анализируем граф цепи. Число неизвестных токов: N_Н= N_В- N_J= 4. Число уравнений по первому закону Кирхгофа: N₁= N_Д= N_У- 1 = 3. Число уравнений по второму закону Кирхгофа: N₂= N_В- N_J- N_У+ 1 = 1.

Уравнения по первому закону Кирхгофа составлены для узлов 1, 2 и 3. Узел 4 – зависимый и для него уравнение не составляется.

Уравнение по второму закону Кирхгофа составляем для единственного главного контура, который образуем присоединением ветви связи 4 к ветвям “дерева” 1, 2 и 5. Направление обхода контура согласуется с направлением ветви 4. Окончательно имеем систему из четырех уравнений –

узел 1	- i₁- i₂+ i₆= 0,
узел 2	i₂- i₃- i₄= 0,	(2.8)
узел 3	i₁+ i₅ - i₆= 0,
контур k	- u₁+ u₂+ u₄+ u₅= 0,

где известны два тока i₃= J₃ и i₆= J₆ и напряжение u₂= e₂.

Система может быть решена относительно неизвестных токов i₁, i₂, i₄, i₅или напряжений u₁, u₄, u₅. Для этого к написанным уравнениям (2.8) необходимо добавить соотношения, связывающие токи и напряжения в каждой отдельной ветви. Их составление показано в следующем разделе.

2.3. Составить уравнения равновесия для электрических цепей, схемы которых представлены на рис. 2 в задаче 2 приложения.

Обобщенная форма закона Ома. Компонентные уравнения

В уравнениях равновесия цепи, составленных по законам Кирхгофа зависимыми переменными являются токи и напряжения. Такие системы называют гибридными. До их решения целесообразно выразить напряжения через токи, либо токи через напряжения, подставить эти выражения в систему и перейти к одному типу переменных. Совокупность таких уравнений, применительно к анализируемой цепи, называются компонентными уравнениями. Каждое из них связывает ток и напряжение в отдельной ветви.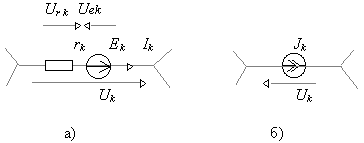

Рис. 2.4. Канонические ветви первого и второго типа

Рассмотрим эти уравнения для канонических ветвей первого (рис. 2.4,а) и второго (рис. 2.4,б) типа.

Для ветви первого типа напряжение ветви U_Kнаходится как разность напряжений на элементе r_k:U_rk= r_k^.I_k и источнике ЭДС U_ek= E_k:

U_k = r_kI_k - E_k или I_k= g_k(U_k+ E_k),

(2.9, 2.10)

где g_k= 1/r_k – проводимость ветви.

Эти соотношения называют обобщенной формой закона Ома. В частном случае, когда E_k= 0, имеем обычную форму закона Ома:

U_k= r_k I_k или I_k= g_kU_k .

В другом случае, когда r_k = 0, получим на основании (2.9)

U_k = - U_ek= - E_k, что действительно имеет место, если направить в одну сторону действие ЭДС и напряжение ветви. Следует особо обратить внимание на то, что знаки в формулах (2.9) и (2.10) непосредственно связаны с условными положительными направлениями тока и напряжений на отдельных участках ветви. Если изменить эти направления, то изменятся и знаки. Поэтому схему рис. 2.4,а можно считать ключевой схемой, ее всегда следует иметь в виду при написании компонентных уравнений.

Для канонической ветви второго типа с источником тока J_k, представленной на рис. 2.4,б, связь между током и напряжением ветви U_k установить невозможно. Это напряжение можно определить только после решения задачи как сумму напряжений ветвей непосредственно примыкающих к источнику тока.

2.4. Составить компонентные уравнения для ветвей схемы на рис. 2.3,а.

В схеме произвольно указаны направления токов и напряжений в каждой ветви. Сравнивая их с направлением стрелок на рис. 2.4, используя формулы (2.9), выражаем напряжения ветвей через токи:

U₁= r₁I₁ - E₁,

U₂= E₂,

(2.11)

U₄= r₄I₄ - E₄,

U₅= r₅I₅ .

Подставив эти выражения в четвертое уравнение системы (2.8), получим систему уравнений относительно четырех неизвестных токов, которую можно решить любым известным способом.

Используя другой вид формул для компонентных уравнений (2.10), выразим токи ветвей через напряжения:

I₁= g₁(U₁+ E₁),

I₄ = g₄(U₄+ E₄),

(2.12)

I₅ = g₅U₅.

После подстановки этих выражений в первые три уравнения системы (2.8), получаем систему уравнений для трех независимых напряжений U₁, U₄ и U₅. Другие напряжения могут быть определены из соотношений:

U₂= E₂; U₃= U₄; U₆= - U₁.

2.5. Для схем на рис.2 задачи 2 приложения указать условные положительные направления токов и напряжений ветвей и составить компонентные уравнения в форме (2.9) и (2.10).

3. РАСЧЕТ РАЗВЕТВЛЕННЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

ПОСТОЯННОГО ТОКА. ПРЯМАЯ И ОБРАТНАЯ ЗАДАЧИ

Ранее было показано, что физические процессы, связанные с движением энергии в электрической цепи, описываются уравнениями равновесия, записанными по законам Кирхгофа. Определение токов и напряжений в ветвях и элементах может быть поставлено в виде прямой или обратной задач. В зависимости от ситуации стратегия их решения может быть различной.

Прямая задача

Прямая задача предполагает заданными параметры источников энергии e, E, j, J и элементов r, L, C электрической цепи. Требуется найти токи и напряжения всех ветвей. В частном случае, при расчете цепей постоянного тока с источниками напряжения и тока E, J требуется только значение сопротивлений r, R. В других случаях, с источниками, напряжения и токи которых изменяются во времени, решение прямой задачи будет рассмотрено далее. В этом параграфе анализируются только цепи постоянного тока.

Прямая задача решается составлением и решением системы алгебраических уравнений. Как было показано, такая задача имеет единственное решение.

3.1. В электрической цепи, схема которой изображена на рис. 3.1 определить токи во всех ветвях. Параметры элементов: r₁= 5[Ом], E₁= 40[B],E₂= 20[B], r₃= 5[Ом], r₄= 20[Ом], E₄= 10[B],r₅= 10[Ом], r₆= 20[Ом], J₆= 3[A].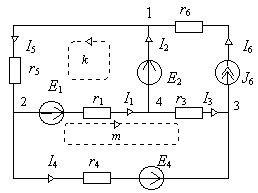

Рис. 3.1

Воспользуемся системой уравнений (2.3), ранее составленной по схеме на рис. 2.1,б

узел 1	- I₂+I₅ - I₆= 0,
узел 2	I₁+I₄ - I₅= 0,
узел 3	- I₃- I₄+ I₆= 0,
контур k	r₁ I₁+ 0 I₂+ r₅ I₅= E₁+ E₂,
контур m	r₁ I₁+ r₃ I₃ - r₄ I₄= E₁ - E₄.

Запишем систему уравнений в матричной форме и перенесем ток

I₆ = J₆в правую часть равенства

Подставляем значения сопротивлений, ЭДС и тока источников

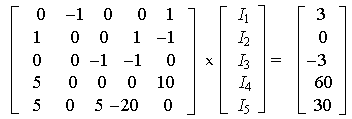
Решая систему уравнений, получаем значения токов: I₁= 3,882[A],

I₂= 1,058[A]I₃= 2,823[A],I₄= 0,1764[A],I₅= 4,058[A]. В пятом разделе пособия показана последовательность решения системы линейных уравнений на ПЭВМ в дисплейном классе кафедры электротехники.

3.2. В электрической цепи рис. 2.3,а определить все токи и напряжения ветвей, полагая: Е₁= 1[В]; Е₂= 5[В]; Е₄= 9[В]; J₃= 3[A]; J₆= 6[A]; r₁= 1[Ом]; r₄= 2[Ом]; r₅= 3[Ом].

Задача сформулирована как прямая, следовательно она имеет единственное решение. Его можно выполнить двумя способами. Первый способ заключается в решении системы уравнений цепи (2.8) при подстановке в них компонентных уравнений в форме (2.11). При этом система сводится к четырем неизвестным токам, а заданные значения токов и ЭДС источников переносятся в правую часть системы:

- I₁- I₂= - J₆,

I₂- I₄= J₃,

I₁+ I₅ = J₆,

- r₁I₁+ r₄I₄+ r₅I₅= - E₁- E₂+ E₄ .

Для решения этой системы на ПЭВМ следует переписать ее в матричной форме

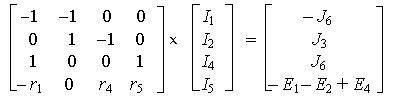
и подставить заданные значения:

Решая систему, находим токи: I₁= 3,5[A]; I₂= 2,5[A]; I₄= - 0,5[A]; I₅=2,5[A]. Знак минус у тока I₄ означает, что его действительное направление противоположно выбранному. Изменять знак тока на обратный до полного решения задачи не следует: это может привести к неверным результатам.

Подставляя полученные токи в компонентные уравнения (2.11), найдем напряжения ветвей: U₁= 2,5[B]; U₂= 5[B]; U₄= 10[B]; U₅= 7,5[B]. Подстановка найденных значений токов и напряжений в систему (2.8) приводит к тождественным равенствам, что подтверждает правильность решения задачи.

Однако не следует смешивать напряжения ветвей с напряжениями на резистивных элементах этих ветвей, которые можно определить по закону Ома:

U_r1= r₁I₁= 3,5 [В]; U_r4 = r₄I₄= 1 [В]; U_r5 = r₅I₅ = 7,5 [В].

Второй способ решения предполагает подстановку компонентных уравнений (2.12) в систему (2.8) и решение ее относительно трех напряжений. Cистема (2.8) включает четыре уравнения. Целесообразно сократить число уравнений до трех так, чтобы исключить из системы ток I₂, который невозможно выразить через напряжение второй ветви. Это можно сделать, суммируя первое и второе уравнения. Тогда система примет вид

- I ₁ - I₄=	J₃ - J₆;
I₁+ I₅=	J₆;
- U₁+ U₄+ U₅=	- E₂.

Подставив в нее выражения (2.8), получаем систему для трех неизвестных напряжений U₁, U₄ и U₅:

- g₁U₁- g₄U₄=	J₃ - J₆+ g₁E₁+ g₄^.E₄,
g₁U₁+ g₅U₅=	J₆ - g₁E₁,
- U₁+ U₄+ U₅=	- E₂,

где g₁= 1/r₁, g₄= 1/r₄, g₅= 1/r₅ проводимости ветвей в [См]. Подставив численные значения и переписав систему в матричной форме, получим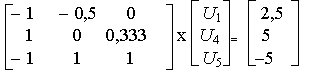

Решая систему, находим: U₁= 2,5[B]; U₄= - 10[B]; U₅= 7,5[B].

Подставив найденные напряжения в выражения (2.12), получим токи: I₁= 3,5[A]; I₄= - 0,5[A]; I₅= 2,5[A]. Ток I₂ вычисляем как алгебраическую сумму токов: I₂= I₄+ J₃= 2,5[A].

Задача решена.

Обратная задача

Обратная задача предполагает известными параметры элементов цепи, значения токов или напряжений в каких либо ее фрагментах. Требуется определить токи, напряжения на других участках цепи и значения токов и напряжений источников питания. Обратная задача может иметь ряд решений, особенно если в цепи действуют несколько источников энергии. Решение обратной задачи не всегда требует составления системы уравнений . Нередко достаточно шаг за шагом определять токи и напряжения других ветвей использованием законов Ома и Кирхгофа.

3.3. Найти токи и напряжения на всех участках электрической цепи и значение напряжения источника питания Е₁ для схемы на рис. 3.1. Параметры цепи: r₁= 1[Oм]; r₂= 2[Ом]; r₃= 2[Ом]; r₄= 5[Ом], Е₂= 10[В] и напряжение U₂= 4[B] на элементе r₂, измеренное вольтметром.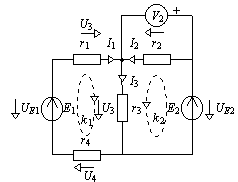

Рис. 3.1

В цепи два источника, поэтому напряжение на элементе r₂ может быть направлено произвольно. Для определенности будем считать, что правая клемма + вольтметра присоединена к общей точке соединения источника E₂ и элемента r₂. Тогда положительное направление напряжения на элементе r₂ будет ориентировано так, как показано на рисунке. Остальные токи и напряжения направляются произвольно, а на источниках напряжений противоположно действию ЭДС. Вольтметр считаем идеальным прибором с бесконечно большим внутренним сопротивлением (r_u= Ґ ).

Решение задачи выполняем последовательными действиями.

1. Определяем значение тока I₂= U₂/r₂= 2[А].

2. Для контура к₂ составляем уравнение по второму закону Кирхгофа и определяем напряжение U₃ :

U₂ - U_E2+ U₃= 0; U₃= - U₂+ E₂= 6[В].

3. По закону Ома находим ток I₃= U₃/r₃= 3[А].

4. По первому закону Кирхгофа определяем ток I₁= I₃- I₂= 1[А].

5.По закону Ома находим напряжения на элементах r₁и r₂:

U₁= r₁^.I₁= 1[В]; U₄= r₄^.I₄= 5[В].

6. Для контура к₁ составляем уравнение по второму закону Кирхгофа и определяем значение E₁

- U_E1+ U₁+ U₃+ U₄= 0; Е₁= U₁+ U₃+ U₄= 12[В].

Задача решена.

3.4. Для электрической цепи, схема которой на рис. 3.2, определить токи и напряжения ветвей и значение тока J источника. Известны сопротивления всех элементов: r₁= 4[Ом]; r₂= 2[Ом]; r₃= 2[Ом]; r₄= 1[Ом] и показание амперметра I₄= 2[А].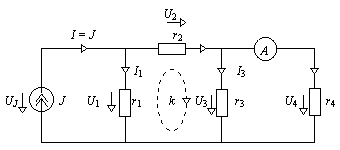

Рис. 3.2

В отличие от предыдущей задачи положительные направления токов и напряжений в данном случае определяются однозначно направлением действия источника. Задача имеет единственное решение, что позволяет легко установить последовательность расчета. Амперметр полагаем идеальным: его внутреннее сопротивление r_{A ®} 0.

1. Находим напряжение U₄= r₄^.I₄= 2[В]. Напряжение U₄= U₃, так как r₃ и r₄ соединены параллельно.

2. Определяем ток в элементе r₃: I₃= U₃/r₃= 1[А].

3. Используя первый закон Кирхгофа, находим I₂= I₃+ I₄= 3[А].

4. Определяем напряжение U₂= r₂^.I₂= 6[В].

5. Из контура к находим напряжение U₁= U₂+ U₃= 8[В]. Это напряжение приложено и к источнику питания.

6. Определяем ток в элементе r₁: I₁= U₁/r₁= 2[А].

7. Аналогично пункту 3 находим ток источника J = I₁+ I₂= 5[А].

Задача решена.

Следствия решения прямой и обратной задач

Решение прямой или обратной задачи позволяет получить значения токов и напряжений на отдельных элементах или ветвях цепи. Далее, используя найденные значения, можно рассчитать следующие характеристики, связанные с распределением электрической энергии по элементам цепи.

1. Расчет мощности, рассеиваемой в резистивных элементах цепи.

2. Определение суммарной рассеиваемой мощности.

3. Определение мощности, которую отдает в цепь источник напряжения или тока.

4. Проверка баланса мощностей.

5. Определение напряжений между любыми узлами.

6. Определение показаний амперметров и вольтметров.

7. Построение потенциальной диаграммы.

1. Рассеиваемая мощность Р [Вт], характеризующая способность резистивного элемента r необратимо преобразовывать электрическую энергию в тепловую и (или) механическую, рассчитывается по любой из формул:

Р = U^.I; P = r^.I² ; P = g^.U²,

(3.1)

где под U следует понимать напряжение на резистивном элементе, а не на всей ветви. При использовании второй формулы путаница исключена.

2.Суммарная рассеиваемая мощность для n резистивных элементов определяется как арифметическая сумма слагаемых (3.1):

3.В цепи с несколькими источниками каждый из них может работать либо в режиме преобразования энергии сторонних сил в электрическую энергию, либо преобразуя электрическую энергию в другие ее виды. В первом случае энергия поставляется электрической цепи, во втором – источник потребляет энергию других источников. Сказанное обязывает определять энергию источника с учетом знака. Для источника напряжения Е на рис. 1.1 мощность P_E, отдаваемая в цепь, определяется формулой

P_E= E I,

(3.3)

где положительные направления тока I и ЭДС Е соответствуют указанным на рисунке. Для источника тока J на рис. 1.1 аналогично имеем соотношение

P_j= JU_j

(3.4)

для положительных направлений тока и напряжения, указанных на рисунке. Если произведение получилось со знаком минус, то источник не отдает энергию в цепь, а берет ее от других источников.

4.Баланс электрических мощностей устанавливается формулой,

где сравнивается сумма мощностей s источников тока и m источников напряжения (с учетом знака) с суммой мощностей, потребляемых в n резистивных элементах цепи. Если задача решена правильно, то баланс будет иметь место.

5. Напряжение между любыми узлами находят на основании второго закона Кирхгофа для любого контура, включающего это напряжение. Необходимо выбирать контур в котором нет ветвей с источниками тока, так как напряжение на этих источниках требует дополнительного определения.

6. Амперметр и вольтметр измеряют значения тока и напряжения. Амперметр включается в разрыв ветви, его сопротивление должно быть много меньше, чем входное сопротивление цепи относительно его зажимов. Идеальный амперметр имеет нулевое внутреннее сопротивление, и его влияние на цепь исключено.

Вольтметр включается параллельно элементу и измеряет напряжение на нем. Для того чтобы не нарушать режим цепи, внутреннее сопротивление вольтметра должно быть много больше входного сопротивления цепи относительно его зажимов. Идеальный вольтметр обладает бесконечно большим внутренним сопротивлением. Если электрическая цепь содержит амперметры и вольтметры, то перед анализом их следует заменить идеальными или реальными моделями.

7. Потенциальная диаграмма графически иллюстрирует распределение потенциала вдоль замкнутого контура цепи. По оси абсцисс откладывают значения сопротивления вдоль этого контура, по оси ординат – потенциалы узлов. Каждому узлу замкнутого контура соответствует своя точка на потенциальной диаграмме. Для построения диаграммы можно выбрать любой контур, составленный ветвями первого типа.

3.5. Проверить баланс мощностей для задачи 3.2.

Решение основывается на значениях токов и напряжений, полученных при решении задачи 3.2 и на уравнении баланса (3.5).

а. Определяем суммарную мощность, которую отдают в цепь источники напряжения:

P_E= P_E1 + P_E2 + P_E4 = E₁I₁ - E₂I₂+ E₄I₄=3,5 - 12,5 - 4,5 = - 13,5[Bт].

Из решения следует, что только источник Е₁ отдает энергию в цепь, а источники Е₂ и Е₄ потребляют ее.

б. Определяем суммарную мощность, которую отдают в цепь источники тока

P_j = P_j3 + P_j6 = - J₃U₄+ J₆U₁= 30 + 15 = 45[Bт] .

Из решения следует, что оба источника тока отдают энергию в цепь.

Сумма мощностей источников энергии:

P_E+ P_j = 45 - 13,5 = 31,5[Вт].

в. Определяем суммарную мощность потерь в резистивных элементах цепи:

P = P_r1 + P_r3 + P_r4 = r₁I₁²+ r₃I₃²+ r₄I₄²=

12,25 + 18,75 + 0,5 = 31,5[Вт].

Результаты расчета показывают, что баланс мощностей имеет место.

3.6. Построить потенциальную диаграмму для схемы цепи рис. 2.3,а и данных задачи 3.2.

Решение задачи начинаем с выбора контура, включающего ветви первого типа. Это единственный контур, составленный ветвями 1, 2, 4 и 5, изображен на рис. 3.3.

Рис. 3.3

В дополнение к нумерации узлов здесь отмечены буквами и простые узлы m и n. В качестве исходного узла, потенциал которого принимаем равным нулю, выбираем четвертый (можно и любой другой). Потенциалы остальных узлов вычисляем последовательно обходя контур с элементами E₄, r₄, E₂, r₁, E₁ и r₅. После каждого шага определяем сумму сопротивлений, которая увеличивается в направлении обхода.

j ₄= 0,

j _n = j ₄+ E₄ = 9 [B],

3. j ₂ = j _{n -}r₄I₄ = 10 [В],

4. j ₁ = j ₂ - E₂ = 5 [В],

5. j _m = j ₁ + r₁I₁ = 8,5 [В],

6. j ₃ = j _m - E₁ = 7,5 [В],

7. j ₄ = j _{3 -}r₅I₅ = 0,

е r_k = 0,

е r_k = r₄ = 2 [Ом],

е r_k = r₄+ r₁ = 3 [Ом],

е r_k = r₄+ r₁+ r₅ = 6 [Ом].

Потенциальная диаграмма изображена на рис. 3.4.

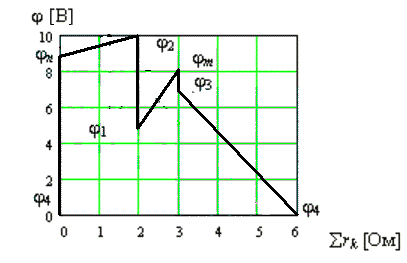
Рис. 3.4

На диаграмме можно определить нужное напряжение как разность потенциалов, оценить наибольшее напряжение.

Изучение материала трех разделов пособия рекомендуем закончить решением третьей и четвертой задач приложения; вариант выбирайте самостоятельно или по рекомендации преподавателя.

4. РАСЧЕТ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА

СИМВОЛИЧЕСКИМ МЕТОДОМ

Если в электрической цепи действуют источники энергии, ЭДС и ток которых изменяется по гармоническому закону

e_k(t) = E_mk Sin(w t + y _ek); J_k(t) = J_mk Sin(w t + y _jk ),

то токи и напряжения на всех участках этой цепи будут гармоническими функциями:

i_k(t) = I_mk Sin(w t + y _ik); u_k(t) = U_mk Sin(w t + y _uk),

где k – номер ветви или элемента. Далее будем полагать, что все источники одной цепи действуют с равной угловой частотой w .

Законы Кирхгофа справедливы для любых цепей и воздействий, в том числе и для цепей синусоидального тока:

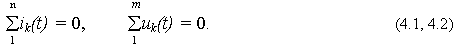
К примеру, определяя для схемы на рис. 4.1,а, токи и напряжения, следует составить два уравнения:

i = i₁+ i₂= I_m1 Sin(w t + y _i1) + I_m2 Sin(w t + y _i2);

u_L= u_r+ u_c= U_mr Sin(w t + y _ur ) + U_mc Sin(w t +y _uc).

Операции с гармоническими функциями в задачах электротехники принципиально проще выполнять, представив их комплексными числами. Такой метод называется символическим или методом комплексных чисел.

В этом методе уравнения (4.1) и (4.2) принимают вид

где I_mk и U_mkкомплексные амплитуды токов и напряжений.

Переход от мгновенных значений к комплексным амплитудам производится следующим образом:

i = I_m Sin(w t + y _i) соответствует I_m= I_me^jy i,

u = U_m Sin(w t + y _u ) соответствует U_m= U_me^jy u,

где I_m и U_m– комплексные числа, записанные в полярной (показательной) форме и сохраняющие информацию об амплитуде и начальной фазе соответствующей синусоидальной функции. Эти числа представляют на комплексной плоскости в виде векторов. Набор векторов, относящихся к данной задаче, образуют векторную диаграмму. На диаграмме комплексные амплитуды токов и напряжений предпочтительно изображать вместе, используя разные масштабы.

Обратный переход от комплексных амплитуд величин к их мгновенным значениям осуществляется по формулам:

i = Jm{I_me ^j(w t + y i)}, u = Jm{U_me ^j(w t + y u) }

(4.5)

где Jm – операция выделения мнимой части комплексной функции.

Переход от схемы анализируемой цепи к комплексной схеме замещения производится на основании таблицы 4.1, где сопротивление каждого элемента заменяется соответствующим комплексным числом:

r – сопротивление резистивного элемента или участка цепи;

jx_L= j(w L) – сопротивление индуктивного элемента;

- jx_c= - j/(w C) = 1/(jw C) – сопротивление емкостного элемента.

В этих соотношениях размерность сопротивления [Ом], индуктивности [Гн] и емкости [Ф].

Возможно использование обратных величин- проводимостей:

g = 1/r – проводимость резистивного элемента или участка цепи;

- jb_L= - j/(w L) = 1/(jw L) – проводимость индуктивного элемента;

jb_C= j(w C) – проводимость емкостного элемента.

Размерность проводимости – сименс [Cм].

В комплексных числах символом j обозначена мнимая единица:

j = e ^j90° ; j²= - 1.

Умножение вектора на ± j, поворачивает этот вектор на угол ± 90° на комплексной плоскости.

Таблица 4.1

Комплексная схема замещения составляется с помощью таблицы 4.1 и анализируется на основании алгебраических уравнений (4.3) и (4.4) т.е. формально решается задача расчета цепи постоянного тока в последовательности ранее детально обоснованной. Отличие лишь в том, что во всех соотношениях вместо E, U, I, r, g будут фигурировать комплексные числа E_m, U_m, I_m, r, jx_L, – jx_c, g, – jb_L, jb_c.

Схема электрической цепи и ее комплексная схема замещения изображены на рис. 4.1,а, 4.1,б. В последней сопротивления элементов и ток источника представлены комплексными числами. Зависимые и независимые переменные связаны системой уравнений

I_m1 + I_m2 = J_m,

U_mr+ U_mc- U_mL= 0,

где токи и напряжения, согласно закона Ома,

U_mr= r I_mr; U_mL= jx_LI_mL; U_mc= - jx_cI_mc.

(4.6)

После подстановки этих соотношений в систему получаем

I_m1+ I_m2= J_m ,

(r - jx_c) I_m1 - jx_L I_m2 = 0.

(4.7)

Рис. 4.1

4.1. Электрическая цепь и ее схема замещения представлены на рис. 4.1,а,б. Параметры: r = 100[Ом]; L = 10[мГн]; C = 1[мкФ], ток источника J(t) = 1,2Sin(10000t – 45⁰)[A]. Определить комплексные амплитуды токов и напряжений; изобразить их векторной диаграммой на комплексной плоскости.

Определяем комплексы сопротивлений и амплитуду тока источника

x_L= w L = 10^{4 .}10 ^.10^-3= 100 [Ом] соответствует z_L= j100,

x_c= 1/w C = 10⁶/(10^{4 .}1) = 100 [Ом] соответствует z_C = - j100,

J(t) = 1,2Sin(10000t – 45⁰) [A] соответствует J_m= I_m= 1,2e^-j45° .

и подставляем их в систему уравнений (4.7). Для вычисления сопротивлений в [Ом] в расчетные соотношения следует подставлять индуктивности в генри [Гн], а емкости в фарадах [Ф].

I_m1 + I_m2 =1,2e^-j45° ,

(100 – j100) I_m1 - j100 I_m2=0.

Полученная алгебраическая система уравнений может быть решена на ПЭВМ или вручную. Комплексные амплитуды искомых токов:

I_m1 = 1,2e^j45° [A]; I_m2 = 1,697e^-j90° [A].

Комплексные амплитуды напряжений на отдельных участках цепи находим на основании выражений (4.6):

U_mr= 120e^j45° [В]; U_mc= 120e^-j45° [В]; U_mL= 169,7[В].

На рис. 4.2 изображены диаграммы токов и напряжений.

Рис. 4.2

Для каждой должен быть указан свой масштаб. Диаграммы могут быть совмещены для оценки фазовых соотношений между векторами и соответствующими им гармоническими функциями.

Рассмотрим иной путь решения задачи 4.1, не требующий составления системы уравнений.

Элементы средней и правой ветвей на схеме рис. 4.1,в имеют значения:

z₁= r₁- jx_c= 100 - j100[Ом] и z₂= jx_L= j100[Ом].

Ветви соединены параллельно; их общее сопротивление равно.

Располагая комплексным сопротивлением z, упрощаем схему: на рис. 4.1,г исходная цепь, не содержащая источников энергии, представлена пассивным двухполюсником.

Определяем напряжение на зажимах двухполюсника; ток I_m= 1,2e^-j45°

U_m= U_m1= U_m2= I_mz = 1,2e^-j45° . 100Ц 2 e ^j45° = 169,7[B].

Возвращаясь к схеме на рис. 4.1,а, находим токи в средней и правой ветвях

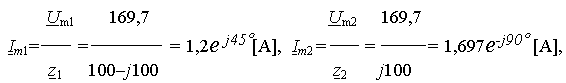
Проверим правильность расчета, используя правило обратной пропорции: значения токов в параллельных ветвях обратно-пропорциональны сопротивлениям этих ветвей –

Значения токов совпадают с полученным ранее решением системы уравнений.

Возможна постановка обратной задачи по расчету цепи синусоидального тока. Далее рассмотрен такой пример.

4.2. Для электрической цепи рис. 4.3,а известна синусоидальная функция тока в емкости i_c= 6Sin(1000t + 30° )[А] и параметры r = 20[Oм], C = 100[мкФ]. Определить комплексные амплитуды токов в ветвях цепи и напряжений на ее элементах.

Решение задачи начинаем с определения комплексных параметров элементов и, обращаясь к таблице 4.1, создаем на рис 4.3,б схему замещения.

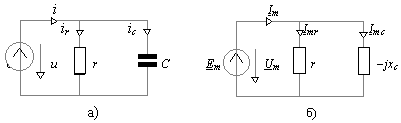
Рис.4.3

x_c= 1/w C = 10⁶/10³ ^.10²= 10[Oм] ё - j10,

i_c= 6Sin(1000t + 30° )[А] ё I_mc= 6e^j30° .

Решение обратной задачи производится так же, как и в цепях постоянного тока шаг за шагом использованием закона Ома и законов Кирхгофа, записанных в комплексной форме (4.3) и (4.4).

а.Определяем комплексную амплитуду напряжения на емкости

U_mc= - jx_c I_mc = - j10 ^. 6e ^j30° = 60e^-j60° [B].

Это напряжение приложено и к резистивному элементу и определяет комплексную амплитуду ЭДС источника E_m= U_mr= U_mc.

б. По закону Ома находим ток в резистивном элементе цепи

I_mr= U_mr/r = 3e^-j60° [A].

в. По первому закону Кирхгофа (4.4) определяем ток источника

I_m= I_mr+ I_mc= 3e^-j60° + 6e^j30° = 6,708e^j3,435° [A].

Суммирование токов показано на векторной диаграмме, приведенной на рис. 4.4, где изображены и вектора напряжений.

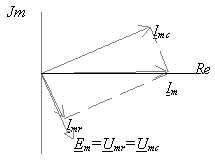
Рис. 4.4

Задача решена.

Следствия решения прямой и обратной задачи

Решение прямой или обратной задачи позволяет определить комплексные значения токов и напряжений отдельных элементов цепи. В дополнение можно рассчитать следующие характеристики.

1. Действующие значения токов и напряжений.

2. Показания вольтметров и амперметров.

3. Активную мощность, потребляемую резистивными элементами или отдаваемую источникам энергии.

4. Реактивную мощность, которая циркулирует между источниками и реактивными элементами цепи.

5. Показания ваттметра.

6. Углы сдвига фаз между токами и напряжениями и другие фазовые соотношения величин.

7. Мгновенные значения токов и напряжений в виде гармонических функций времени.

1,2. Амперметры и вольтметры, измеряющие токи и напряжения изменяющиеся во времени по гармоническому закону, градуированы в действующих значениях этих величин. Действующее значение отличается от амплитудного множителем :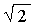

I = I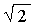_m / , U = U_m /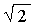

(4.8)

Из выражений (4.8) следует, что показание какого-либо прибора равно модулю комплексной амплитуды поделенной на .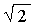

3. Мощность, потребляемая резистивными элементами или двухполюсниками, вычисляется по любой из формул:

P = r I²; P = g U²; P = U I,

(4.9)

где U,I – действующие значения напряжения и тока.

Анологично для определения реактивной мощности в индуктивных и емкостных элементах имеем

Q_L,C= ± U I; Q_L,C = ± x_L,CI²; Q_L,C= ± b_L,CU²,

(4.10)

где знак плюс (+) приписывается индуктивности, а знак минус (–) емкости.

4. Для вычисления активной и реактивной мощности в ветви, характеризуемой комплексным сопротивлением z или проводимостью y, используют формулы

P = U I cosφ; P = Re(U I); Q = U I sinφ; Q = Jm(U I),

(4.11)

где φ = Ψ_u– Ψ_i– угол сдига фаз между током и напряжением ветви, I = Ie^-jΨi – комплексно-сопряженное току I = Ie^jΨi

5. Измерение мощности ваттметром рассмотрим подробнее. Напряжение и ток ветви или цепи (рис. 4.5)

u(t) = U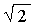 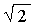Sin(w t + y _u), i(t) = ISin(w t+y _i).

Мгновенной мощностью называют произведение

P = ui = U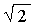Sin(w t + y _u) ISin(w t + y _i) =

UICosj - UICos(2w t + y _u+ y _i), где j = y _u- y _i.

Среднее значение мгновенной мощности P = UICosj измеряют ваттметром. Величину P называют активной мощностью, ее размерность – ватты [Вт].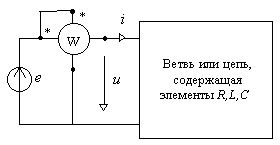

Рис. 4.5

Ваттметр (рис. 4.5) имеет две обмотки – напряжения и тока, начала обмоток помечены звездочкой. В зависимости от порядка включения обмоток, стрелка прибора может отклонятся в ту или иную сторону. Если начала обмоток соединены и расположены со стороны источника, то отклонение стрелки вправо свидетельствует о потреблении пассивным двухполюсником энергии источника. Если на схеме рис. 4.5 полагать, что ветвь или цепь содержат источники энергии, то отклонение стрелки ваттметра влево имело бы место лишь в том случае, когда источник e(t) не отдает, а потребляет энергию.

6. Фазовые соотношения определяются разностью начальных фаз напряжений и(или) токов. Для этого вычисляется разность аргументов этих величин, записанных в экспоненциальной форме.

7. Мгновенные значения – синусоидальные функции токов и напряжений определяются формулами (4.5).

4.3 Используя результаты решения задачи 4.1, определить действующие значения токов и напряжений, активную и реактивную мощность в цепи.

Действующие значения определяем по формулам (4.8):

I = 1,2/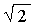 = 0,8485[A], I₁= 1,2/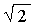=0,8485[A], I₂= 1,697/ 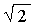= 1,2[A],

U_L= 169,7/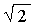 = 120[B], U_r= 120/ 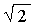= 84,85[B], U_c= 120/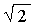= 84,85[B].

На схеме рис.4.1.a имеет место единственный резистивный элемент, который рассеивает активную мощность. Ее можно определить по одной из формул (4.9)

P = r I₁²= 100 ^. (0,8485)²= 72 [Вт].

Воспользуемся и более общей формулой, рассматривая всю цепь как двухполюсник по отношению к источнику питания:

P = U I Cosj = U_L I cos(y _uL – y _i) = 120 ^. 0,8485 ^. Cos(45° )=72[Вт].

Результаты расчета совпадают.

Для определения реактивной мощности используем формулы (4.10).

Как и ранее, можно определить эту мощность отдельно для индуктивности и для емкости, затем алгебраически суммировать результаты:

Q_L = x_L I₂²= 100 ^. (1,2)²= 144 [BAр],

Q_c = - x_c I₁² = - 100 ^. (0,8485)²= - 72 [BAp],

Q = Q_L+ Q_c = 72 [BAp].

Рассматривая цепь как двухполюсник, найдем мощность Q иначе:

Q = U I Sinj = U_L I Sin(y _uL – y _i) = 120 ^. 0,8485 ^.Sin(45° ) = 72 [BAp].

Результаты совпадают и задача решена.

4.4. Используя результаты решения задачи 4.2, записать мгновенное значение тока i_r(t) и построить график этой функции.

Воспользовавшись формулой (4.5), запишем

i_r(t) = Jm{I_me^j(w t + y i)} = Jm{3e^j(1000t – 60° )} = 3Sin(1000t – 60° )[A].

Рис. 4.6

На рис. 4.6 изображён график синусоидальной функции тока в резистивном элементе. Ее смещение вправо относительно начала координат обусловлено отрицательным значением начальной фазы y _i = - 60° .

Задача решена.

4.5. Для цепи (рис. 4.7,а), подключённой к источнику напряжения e(t) с частотой f, известны показание вольтметра U₂= 50[B] и значения сопротивлений r₁ = 10[Ом], r₂ = 40[Ом], x_c1 = 40[Ом], x_c2 = 10[Ом].

Необходимо определить следующие значения величин.

а. Показание амперметра А.

б. Показания вольтметров V₁ и V.

в. Показание ваттметра W.

г. Угол сдвига фаз между током I и напряжением U₁ .

д. Угол сдвига фаз между напряжениями U и U₁ .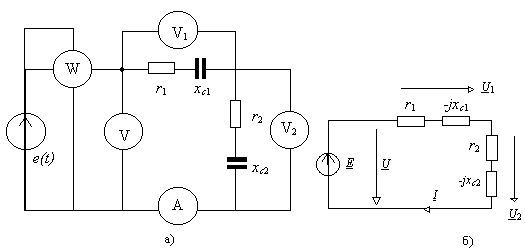

Рис. 4.7

Решение задачи начинаем с составления комплексной схемы замещения на рис. 4.7,б. Амперметр и вольтметры заменяем идеальными моделями: R_A® 0, R_V® 0. Аналогично исключаем влияние обмоток ваттметра: сопротивление обмотки тока R_I® 0, сопротивление обмотки напряжения R_U® 0. На схеме замещения указывам положительные направления тока и напряжений подлежащих определению. В решении будем оперировать действующими значениями величин: приборы градуированы и измеряют именно эти значения. Начальные фазы токов и напряжений могут быть определены относительно начальной фазы любой величины. В данной задаче выбираем в качестве исходной начальную фазу y _u2 напряжения U₂ и полагаем её равной нулю:

y _u2= 0, U₂ = U₂eⁱy u2 = 50eⁱ0 = 50[B].

Комплексные сопротивления емкостей

- jx_c1 = - j40 [Ом], - jx_c2 = - j10 [Ом].

Задачу решаем как обратную рядом последовательных шагов.

а. По закону Ома для участка цепи определяем комплекс действующего значения тока

Амперметр показывает значение равное модулю комплекса тока

I = | I | = 1,21 [A].

б. По закону Ома определяем напряжение U₁

U₁= U₁e^jy u = Z₁I = (r₁- jx_c1) I = (10 - j40) ^. 1,21e^j14° =

41,e^–j76° . 1,21e^j14 ° = 50e^–j62° [B].

Вольтметр V₁ измеряет модуль комплексного числа U₁= | U₁|=50[B].

Напряжение U определяем по второму закону Кирхгофа как сумму напряжений

U = U₁+ U₂= 50 + 50e^–j62° = 50(1 + Cos62° ^- jSin62° ) =

= 50(1+ 0,469- j0,829) = 50 ^. 1,714e^–j31° = 85,7e^–j31° [B].

Вольтметр V измеряет модуль этого значения U =| U |= 85,7[B].

Предлагаем обратить внимание на следующее. Определяя напряжение U, мы суммировали комплексы напряжений U₁ и U₂, а не показания вольтметров V₁ и V₂.

в. Ваттметр определяет значение мощности, которую вычисляем по формуле

P = U I Cosj = 85,7 ^. 1,21 ^. Cos(- 45° ) = 73,54 [Вт],

где j = y _u - y _i= - 31° - 14° = - 45° .

Аналогичный результат получим, суммируя мощности, рассеиваемые в элементах r₁ и r_{2 -}

P = P₁+ P₂= r₁ I²+ r₂ I²= (r₁ + r₂) I²= 50 ^. (1,21)²= 73,32 [Bт].

г. Угол сдвига фаз между током I и напряжением U₁ находим как разность аргументов соответствующих комплексных чисел

j ₁= y _u1 - y _i= - 62° - 14° = - 76° ,

т.е. ток опережает по фазе напряжение U₁ на 76° . Это же значение соответствует аргументу сопротивления Z₁= 41,2e ^– j76° [Ом].

д. Угол сдвига фаз между напряжениями U и U₁ определим как разность аргументов соответствующих комплексных чисел

y ₂= y _u - y _u1 = - 31° + 62° = 31° .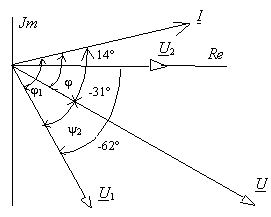

Рис.4.8

Векторная диаграмма токов и напряжений, вычисленных в данной задаче, представлена на рис. 4.8, где указаны фазовые соотношения величин.

Задача решена.

4.6. Схема электрической цепи представлена на рис. 4.9. Ее параметры: e₁(t) = 5Sin1000t [B], e₂(t) = 4Ц 2 Sin(1000t + 45° )[B], j(t) = 3Sin(1000t + 90° )[A], r₁= r₃= 1[Ом], r₂= r₄= 2[Ом], C = 500[мкФ],

L₁= 3[мГн], L₂= 2[мГн]. Определить комплексы амплитудных значений токов во всех ветвях цепи.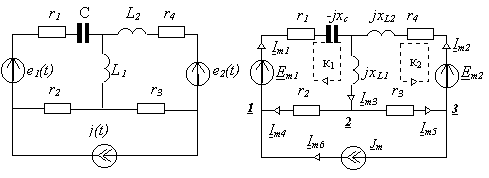

Рис. 4.9

Рис. 4.10

Рисуем схему замещения (рис. 4.10), используя таблицей 4.1. В схеме четыре узла N_У= 4, шесть ветвей N_B= 6, одна ветвь содержит источник тока N_J = 1. Во всех ветвях, кроме одной, указываем положительные направления токов и нумеруем их I_m1ё I_m6; ток I_m6 направляем по действию источника тока. По первому закону Кирхгофа составляем три уравнения

N₁= N_У- 1 = 4 - 1 = 3 для узлов 1, 2 и 3. По второму закону Кирхгофа составляем два уравнения N₂= N_В- N_J- (N_У- 1) = 6 - 1 - (4 - 1) = 2 для контуров к₁и к₂не содержащих ветвь с источником тока.

Получаем систему из пяти уравнений

узел 1	I_m1- I_m4- I_m6= 0,
узел 2	- I_m3+ I_m4+ I_m5= 0,
узел 3	I_m2- I_m5+ I_m6= 0,
контур к₁	(r₁- jx_c)I_m1+ jx_L1I_m3+ r₂I_m4= E_m1,
контур к₂	(r₄+ jx_L2)I_m2+ jx_L1I_m3+ r₃I_m5= E_m2, где I_m6= J_m.

Определяем сопротивления элементов

x_L1= w L₁= 1000 ^.0,003 = 30[Ом], x_L2= w L₂= 1000 ^.0,002 = 2[Ом],

x_С= 1/(w C) = 1/(w C) = 1/(1000 ^.500 ^.10^-6) = 2[Ом].

Представляем их и гармонические функции трех источников комплексными числами

jx_L1= j3[Ом], jx_L2= j2[Ом], – jx_C= – j2[Ом], r₁= r₃= 1[Ом],

r₂= r₄= 2[Ом], E_m1 = 5[B], E_m2= 4Ц 2 e^j45° = (4+j4)[B], J_m= 3e^j90° = j3[A].

Подставив значения величин в систему уравнений, записываем последние в матричной форме

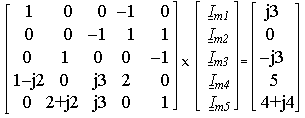
Решая систему, находим токи: I_m1= 1,497e^j57° [A],I_m2= 1,355e^-j69,6°[A],

I_m3= 1,288e^-j0,631° [A], I_m4= 1,925e^-j64,9°[A], I_m5= 1,794e^j74,7° [A].

В пятом разделе пособия показана последовательность использования ПЭВМ для решения системы линейных уравнений.

4.7. В последовательной r,L цепи (рис. 4.11,а) известны показания вольтметров U₁= 100[B], U₂= 150[B], сопротивление r = 10[Ом] и частота источника питания f = 50[Гц]. Определить показание третьего вольтметра U[B] и индуктивность элемента L[Гн].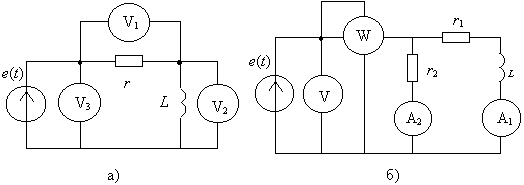

Рис.4.11

4.8. Определить показания приборов в цепи (рис. 4.11,б). Известно показание первого амперметра I₁= 1[A] и параметры элементов:

r₁= 100[Ом], r₂= 200[Ом], L = 0,276[Гн], f = 100[Гц].

Изучение материала четвертого раздела пособия рекомендуем закончить решением пятой задачи приложения; вариант выбирайте самостоятельно или по рекомендации преподавателя.
5. РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ НА ПЭВМ

В качестве первого примера обратимся к системе уравнений в матричной форме, составленных в задаче 3.2 пособия по расчету цепи постоянного тока

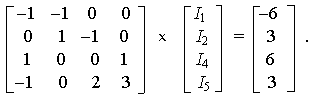
Решение выполняем на машине в классе персональных ЭВМ кафедры электротехники в следующей последовательности.

После включения ПЭВМ преподавателем или лаборантом, загрузки и самотестирования, последовательно выбираем в предлагаемых меню: “Сервисные и расчетные программы”, “Решение системы линейных уравнений”, клавишей перемещения курсора по экрану указываем порядок матрицы равный количеству уравнений системы; в примере он равен четырем. Очередной выбор или действие завершаем командой ВВОД (ENTER). На экране дисплея

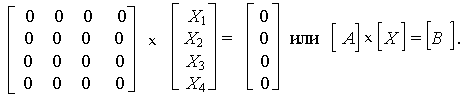
Первоначально элементы матриц A,Bравны нулю.

Мигающий элемент матрицы А готов к заполнению. Набираем его значение с помощью клавиатуры, разделяя целую и дробную части числа точкой. Завершаем набор нажимая клавишу ВВОД. Вместо мигающего элемента – ромбик: элемент имеет значение. Переходим на соседние элементы, используя клавиши перемещения курсора, и вводим их значения. Переход к элементам матрицы В выполняем, нажимая клавишу табуляции (ТАБ).

Проверяем правильность введенных значений. Для перехода в этот режим нажимаем одновременно две клавиши Э (SHIFT) и F8. Используя клавиши перемещения курсора по экрану, переходим от элемента к элементу матрицы, проверяя их значения. Исправить ошибку можно вернувшись в режим ВВОД, нажав клавишу F8. С помощью клавиш перемещения курсора выбираем нужный элемент и вводим его правильное значение.

Решение системы уравнений рассматриваемого примера получаем одновременно нажав клавиши CTRL и F8. Вот оно:

X₁ = I₁= 3,5[A], X₂ = I₂= 2,5[A], X₃ = I₄= - 0,5[A], X₄ = I₅= 2,5[A].

В качестве второго примера рассмотрим систему уравнений с комплексными коэффициентами в матричной форме записи, составленную к задаче 4.6 по расчету цепи переменного тока.

Универсальный калькулятор выполняет операции и с комплексными числами. Комплексное число записывается либо в алгебраической форме: 1 - j2, либо в полярной: 2,23e^–j53,44°; оба числа равны и взяты в качестве примера. Вводим первое: набираем единицу, минус, число j вводит программа, набираем двойку, нажимаем клавишу ВВОД. Ввод второго: набираем два, точку, двадцать три, символ угла, число j вводит программа, минус, пятьдесят три, точку, сорок четыре, нажимаем клавишу ВВОД. При необходимости ввода числа j3 набираем: символ j, три, нажимаем клавишу ВВОД.

Решение выполняем в последовательности приведенной в первом примере. Вводим значения элементов матриц А, В и проверяем их правильность. Решая систему, получаем комплексы амплитудных значений токов

I_m1= 1,497e ^j57° [A],I_m2= 1,355e ^-j69,6° [A], I_m3= 1,288e ^-j0,631° [A],

I_m4= 1,925e ^-j64,9° [A], I_m5= 1,794e ^j74,7° [A].

Значения токов могут быть определены и в алгебраической форме:

I_m1= 0,8154 + j1,255 [A], I_m2= 0,4726 – j1,269 [A],

I_m3= 1,288 – j0,0142 [A], I_m4= 0,8154 – j1,744 [A],

I_m5= 0,4726 + j1,730 [A].

В библиотеке ИТМО можно взять учебное пособие [10] и прилагаемую к нему дискету с комплексной программой для инженерных расчетов А.А. Усольцева.

Приложение

Задача 1. Электрическую цепь, варианты схем которой изображены на рис. 1, упростить до одного элемента по отношению к зажимам источника питания u. Значения параметров приведены в таблице 1 для каждого варианта.

Рис. 1

Таблица 1

Вариант	Рисунок	Параметры элементов цепи r [Ом], L[Гн], Cґ 10^–6[Ф]	Определить r_э, L_э, C_э
1	а	C₁=1, C₂=1, C₃=2,C₄=2, C₅=2, C₆=7, C₇=3	C_э
2	б	L₁=1, L₂=1, L₃=4,L₄=4, L₅=4, L₆=7, L₇=1	L_э
3	г	C₁=30, C₂=10, C₃=10,C₄=20, C₅=10	C_э
4	д	L₁=1, L₂=2, L₃=2,L₄=4, L₅=3	L_э
5	ж	C₁=6, C₂=6, C₃=12,C₄=9, C₅=6, C₆=6	C_э
6	з	L₁=4, L₂=4, L₃=12,L₄=8, L₅=4, L₆=4	L_э
7	к	C₁=2, C₂=2, C₃=12,C₄=8, C₅=8, C₆=8	C_э
8	л	L₁=4, L₂=4, L₃=10,L₄=6, L₅=9, L₆=1	L_э
9	н	C₁=2, C₂=4, C₃=2,C₄=4, C₅=4, C₆=8	C_э
10	о	L₁=1, L₂=1, L₃=1,L₄=1, L₅=1, L₆=1	L_э
11	в	r₁=8, r₂=8, r₃=6,r₄=4, r₅=4	r_э
12	е	r₁=5, r₂=1, r₃=4,r₄=4, r₅=2	r_э
13	и	r₁=4, r₂=3, r₃=6,r₄=6, r₅=3	r_э
14	м	r₁=3, r₂=6, r₃=2,r₄=6, r₅=3	r_э
15	п	r₁=3, r₂=6, r₃=2,r₄=4, r₅=1, r₆=5	r_э
16	р	r₁=2, r₂=2, r₃=2,r₄=3, r₅=3, r₆=3	r_э
17	а	C₁=6, C₂=1, C₃=3,C₄=2, C₅=4, C₆=6, C₇=5	C_э
18	б	L₁=1, L₂=2, L₃=8,L₄=3, L₅=6, L₆=7, L₇=4	L_э
19	г	C₁=10, C₂=3, C₃=5,C₄=2, C₅=5	C_э
20	д	L₁=4, L₂=12, L₃=12,L₄=12, L₅=8	L_э
21	ж	C₁=4, C₂=8, C₃=8,C₄=12, C₅=5, C₆=7	C_э
22	з	L₁=3, L₂=6, L₃=3,L₄=2, L₅=3, L₆=6	L_э
23	к	C₁=6, C₂=3, C₃=6,C₄=6, C₅=6, C₆=6	C_э
24	л	L₁=6, L₂=3, L₃=2,L₄=6, L₅=1, L₆=3	L_э
25	н	C₁=2, C₂=4, C₃=2,C₄=4, C₅=4, C₆=8	C_э

Задача 2. Для электрической цепи, варианты схем которой изображены на рис. 2, определить входное сопротивление R_вх относительно каждой из двух ветвей, номера которых указаны в четвертом столбце таблицы 2.

Значения параметров элементов для каждого варианта приведены в таблице 2.

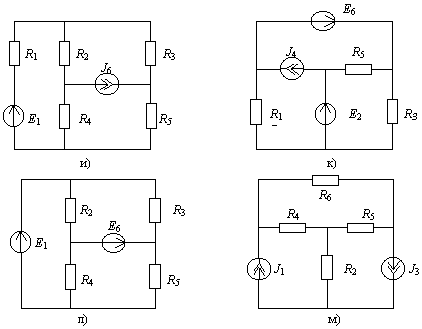
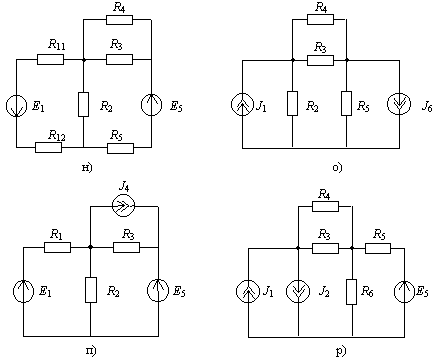
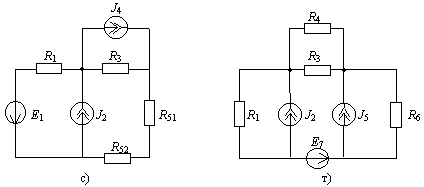
Рис. 2

Таблица 2

Вар.

Рис.

Параметры сопротивлений и источников

R [Ом] E[B] J[A]

Номера ветвей

Определить

I, U, P

1

а

R₁=1, R₂=2, R₃₁=2, R₃₂=4, E₁=10, E₂=20

1,2

I₁, U₂, P_E2

2

б

R₂₁=3, R₂₂=4, R₃=2, E₃=4,5, J₁=0,2

2,3

I₃, U₂, P_J1

3

в

R₁₁=2, R₁₂=3, R₂₁=6, R₂₂=4,

E₁=15, E₂=45, J₃=0,3

1,2

I₂, U₃, P_R12

4

г

R₁=2, R₃₁=1, R₃₂=2, R₃₃=3, E₁=16, J₂=0,4

1,3

I₁, U₃₁, P_E1

5

д

R₁=1, R₂=4, R₃=3,

E₁₁=24, E₁₂=1, E₁₃=6, E₂=19, E₃=38

2,3

I₂, U₃, P_E3

6

е

R₁₁=1, R₁₂=3, R₂₁=2, R₂₂=2, R₃=5,

E₁₁=14, E₁₂=7, E₃₁=9, E₃₂=2

2,3

I₃, P_E31, P_R22

7

ж

R₂=2, R₃=3, R₄=4, R₅=5, J₁=0,1, J₆=0,5

4,5

I₂, P_J1, P_J6

8

з

R₂=1, R₃=5, R₄=4, R₅=3, E₆=28, J₁=0,9

2,6

I₄, P_J1, P_E6

9

и

R₁=2, R₂=4, R₃=4, R₄=2, R₅=6, E₁=12, J₆=0,4

1,3

I₃, U₅, P_R4

10

к

R₁=2, R₃=5, R₅=6, E₂=26, E₆=52, J₄=7

1,5

I₅, I₆, P_E6

11

л

R₂=2, R₃=1, R₄=4, R₅=5, E₁=13, E₆=26

1,4

I₂, U₅, P_E1

12

м

R₂=6, R₄=4, R₅₌5, R₆=1, J₁=2, J₃=5

4,6

U_J1, U₄, P_R6

13

н

R₁₁=3, R₁₂=1, R₂=2, R₃=2, R₄=2, R₅=4,

E₁=19, E₅=38,

1,4

I₂, U₄, P_E5

14

о

R₂=1, R₃=2, R₄=5, R₅=4, J₁=7, J₆=21

4,5

I₃, U₂, P_J1

15

п

R₁=3, R₂=4, R₃=6, E₁=54, E₅=36, J₄=3,

1,2

I₁, U₃, P_R1

16

р

R₃=3, R₄=6, R₅=3, R₆=6, E₃=9, J₁=0,5, J₂=1,5

4,6

I₃, U₆, P_J2

17

с

R₁=1, R₃=4, R₅₁=3, R₅₂=2,

E₁=10, J₂=0,2, J₄=0,4

1,3

I₁, U₂, P_E1

18

т

R₁=1, R₃=6, R₄₌3, R₆=5,

E₇=16, J₂=0,5, J₅=0,2

4,6

I₆, U₃, P_R3

19

з

R₂=2, R₃=6, R₄₌3, R₅=4, E₆=16, J₁=0,4

2,3

I₄, U₂, P_J1

20

и

R₁=4, R₂=1, R₃₌2, R₄=3, R₅=3, E₁=56, J₆=4,5

3,4

I₅, U₄, P_E1

21

л

R₂=4, R₃=2, R₄=1, R₅=5, E₁=13, E₆=39

1,5

I₄, I₆, P_R2

22

н

R₁₁=1, R₁₂=2, R₂₌2, R₃=3, R₄=6, R₅=1,

E₁=21, E₅=14,

4,5

I₅, U₅, P_E1

23

о

R₂=2, R₃=1, R₄=5, R₅=3, J₁=0,2, J₆=12

2,3

I₅, U₆, P_J6

24

т

R₁=4, R₃=6, R₄=3, R₆=2,

E₇=16, J₂=0,5, J₅=0,3

3,7

I₇, U₆, P_R1

25

ж

R₂=2, R₃=3, R₄₌1, R₅=4, J₁=1, J₆=3

2,5

I₅, U₂, U₆

Задача 3. В электрической цепи известны параметры источников и пассивных элементов. Определить: значения токов в ветвях, напряжения на резистивных элементах цепи; суммарную мощность, отдаваемую источниками энергии; суммарную мощность, рассеиваемую элементами цепи. Составить баланс мощностей. Построить потенциальную диаграмму для любого замкнутого контура, содержащего два источника ЭДС.

Цепь представлена пятью формальными вариантами схем без элементов. Перед анализом необходимо скомпоновать схему варианта цепи, дополнив формальную структуру источниками и элементами. В каждой ветви: источник и резистивный элемент; один из них может отсутствовать. В таблице 3 приведены параметры источников. Номера тока и ЭДС источников совпадают с номерами тех ветвей в которых эти источники должны быть расположены; стрелками указаны направления действия источников. В таблице 4 приведены параметры резистивных элементов.

В качестве примера показана компоновка схемы 25-го варианта.

Таблица 3

Таблица 4

Вариант	Ветвь 1	Ветвь 2	Ветвь 3	Ветвь 4	Ветвь 5	Ветвь 6
1	R₁=30	R₂=9	R₃=8	R₄=9	R₅=5
2	R₁=0	R₂=8	R₃=9	R₄=5	R₅=6	R₆=7
3	R₁=32	R₂=3	R₃=4	R₄=7	R₅=6	R₆=9
4	R₁=34	R₂=8	R₃=7	R₄=2	R₅=9
5	R₁=36	R₂=6	R₃=4	R₄=2	R₅=3	R₆=8
6	R₁=9	R₂=7	R₃=0	R₄=10	R₅=8
7	R₁=8	R₂=6	R₃=11	R₄=5	R₅=10	R₆=9
8	R₁=10	R₂=9	R₃=14	R₄=6	R₅=11	R₆=0
9	R₁=32	R₂=0	R₃=8	R₄=9	R₅=7
10	R₁=6	R₂=5	R₃=8	R₄=9	R₅=10	R₆=12
11	R₁=12	R₂=7	R₃=6	R₄=8	R₅=0
12	R₁=9	R₂=5	R₃=14	R₄=8	R₅=6	R₆=22
13	R₁=24	R₂=8	R₃=0	R₄=10	R₅=7	R₆=14
14	R₁=0	R₂=6	R₃=13	R₄=6	R₅=14
15	R₁=16	R₂=9	R₃=10	R₄=8	R₅=12	R₆=26
16	R₁=7	R₂=16	R₃=5	R₄=8	R₅=14
17	R₁=0	R₂=9	R₃=12	R₄=7	R₅=8	R₆=16
18	R₁=10	R₂=7	R₃=9	R₄=5	R₅=12	R₆=6
19	R₁=15	R₂=8	R₃=6	R₄=12	R₅=9
20	R₁=7	R₂=13	R₃=6	R₄=15	R₅=8	R₆=9
21	R₁=9	R₂=12	R₃=17	R₄=10	R₅=8
22	R₁=14	R₂=6	R₃=10	R₄=8	R₅=0	R₆=9
23	R₁=13	R₂=7	R₃=11	R₄=9	R₅=6	R₆=0
24	R₁=5	R₂=9	R₃=10	R₄=4	R₅=7
25	R₁=5	R₂=10	R₃=15	R₄=40	R₅=12	R₆=9

В таблице 4 значения сопротивлений R указаны в омах.

Задача 4. Варианты схем электрической цепи приведены на рис. 2. Определить токи, напряжения и мощности в элементах, номера которых приведены в пятом столбце таблицы 2. Параметры элементов цепи приведены в таблице 2.

Задача 5. В цепи известны параметры источников и элементов.

Определить:

а) комплексные амплитудные значения токов в ветвях;

б) комплексные амплитудные значения напряжений на пассивных элементах, входящих в один произвольно выбранный замкнутый контур цепи;

в) построить в масштабе векторную диаграмму токов для любого узла электрической цепи;

г) построить в масштабе векторную диаграмму напряжений для выбранного в пункте б) контура;

д) любое комплексное амплитудное значение тока, рассчитанное в пункте а), и напряжения, рассчитанное в пункте б), записать в виде мгновенных значений и представить графически эти две функции времени в подходящем масштабе.

е) определить действующие значения тока и напряжения из пункта д);

ж) рассчитать активную мощность Р, потребляемую любым резистивным элементом и реактивную мощность Q, запасаемую индуктивным или емкостным элементом.

Каждый вариант схемы содержит пять – шесть ветвей, изображенных без элементов. В ветви: один источник (он может отсутствовать) и один – два пассивных элемента. В таблице 5 приведены параметры источников; их в схеме три. Номера тока и ЭДС источников совпадают с номерами тех ветвей в которых эти источники должны быть расположены; стрелками указаны направления действия источников. В таблице 6 приведены параметры пассивных элементов. Перед анализом необходимо скомпоновать самостоятельно схему варианта цепи, дополнив формальную структуру источниками и элементами. В качестве примера показана схема первого варианта.

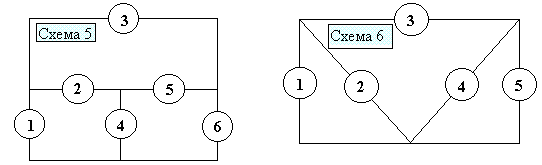
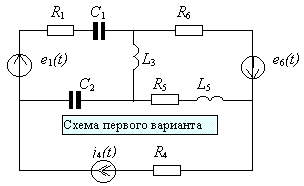
Таблица 5

Таблица 6

Параметры элементов ветвей R[Ом], Lґ 10^–3[Гн], Cґ 10^–6[Ф]

вариант
Я	Ветвь 1	Ветвь 2	Ветвь 3	Ветвь 4	Ветвь 5	Ветвь 6
1	R=3, C=10⁴	C=5^.10³	L=10	R=20	R=4, L=40	R=4
2	Элементов нет	R=8, C=10³	R=6	C=500	R=10	R=5, L=10
3	R=50	R=4, C=1250	C=625	R=2, L=10	L=5	-
4	R=100	R=6, C=1000	Элементов нет	R=8	C=1250	R=4, L=120
5	R=2, L=10	Элементов нет	L=4	R=5	R=4, C=400	-
6	R=40	R=6, C=625	R=5	R=3, L=50	R=4	L=40
7	Элементов нет	R=6, L=40	R=4	L=50	C=2500	R=5, C=2000
8	R=5, C=312,5	C=250	Элементов нет	R=7	R=6	R=10, L=12,5
9	R=6, L=10	R=4	C=500	R=8, C=250	R=5	-
10	C=1000	R=5	R=4, L=20	R=3, C=500	R=8	Элементов нет
11	Элементов нет	R=8, L=5	L=8	R=4	R=6, C=250	R=5
12	R=8, L=8	L=10	R=6, C=250	R=4	Элементов нет	-
13	R=5	R=3, C=1250	C=5000	R=4	L=5	Элементов нет
14	R=6, L=8	R=8	Элементов нет	C=2000	R=4, C=200	R=2
15	R=3, L=16	Элементов нет	R=6	R=60	L=2	R=4, C=1000
16	R=4, C=2500	C=500	L=20	R=8	R=5	L=2,5
17	C=2000	R=4, C=4000	R=6	R=5	R=3, L=20	-
18	Элементов нет	R=5	R=7, C=500	C=125	R=4	R=8, L=12
19	R=2, L=4	R=4	L=8	Элементов нет	R=6	R=5, C=500
20	R=80	R=5	R=4, C=200	R=3, L=2	Элементов нет	L=4
21	C=250	R=6, L=20	C=500	R=8	Элементов нет	L=20
22	R=20	R=6, L=25	Элементов нет	C=2500	R=4, C=1250	-
23	R=4, C=500	C=1000	L=20	R=4, L=20	Элементов нет	-
24	R=6, L=25	L=12,5	R=8	R=5, C=625	R=4	Элементов нет
25	R=6, L=16	L=32	C=400	R=7	C=4000	R=8

Список литературы

1. Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. – М.: Высшая школа, 1978.

2. Зевеке Г. Ф. и др. Основы теории цепей. Учебник для вузов. – М.: Энергоатомиздат, 1989.

3. Нейман Л. Р., Демирчян К.С. Теоретические основы электротехники. В двух томах. Том 1. Учебник для вузов. – Л.: Энергоатомиздат, 1981.

4. Матханов П. Н. Основы анализа электрических цепей. Линейные цепи. – М.: Высшая школа, 1980.

5. Глазенко Т. А., Прянишников В. А. Электротехника и основы электроники. Учебное пособие для вузов. – М.: Высшая школа, 1985.

6. Касаткин А. С. Электротехника. – М.: Энергия, 1973.

7. Общая электротехника. Учебное пособие для вузов. /Под редакцией А. Т. Блажкина/. – Л.: Энергоатомиздат, 1986.

8. Новгородцев А.Б. 30 лекций по теории электрических цепей.

– Спб.: Политехника, 1995.

9. Прянишников В.А. Теоретические основы электротехники.

Курс лекций. – СПб.: Корона принт, 2000.

10. Прянишников В.А., Петров Е.А., Осипов Ю.М. Электротехника

и ТОЭ в примерах и задачах. Практическое пособие – Спб.:

Корона принт, 2001.

U₁= r₁I₁ - E₁,
U₂= E₂,	(2.11)
U₄= r₄I₄ - E₄,
U₅= r₅I₅ .

I₁= g₁(U₁+ E₁),
I₄ = g₄(U₄+ E₄),	(2.12)
I₅ = g₅U₅.

Вар.	Рис.	Параметры сопротивлений и источников R [Ом] E[B] J[A]	Номера ветвей	Определить I, U, P
1	а	R₁=1, R₂=2, R₃₁=2, R₃₂=4, E₁=10, E₂=20	1,2	I₁, U₂, P_E2
2	б	R₂₁=3, R₂₂=4, R₃=2, E₃=4,5, J₁=0,2	2,3	I₃, U₂, P_J1
3	в	R₁₁=2, R₁₂=3, R₂₁=6, R₂₂=4, E₁=15, E₂=45, J₃=0,3	1,2	I₂, U₃, P_R12
4	г	R₁=2, R₃₁=1, R₃₂=2, R₃₃=3, E₁=16, J₂=0,4	1,3	I₁, U₃₁, P_E1
5	д	R₁=1, R₂=4, R₃=3, E₁₁=24, E₁₂=1, E₁₃=6, E₂=19, E₃=38	2,3	I₂, U₃, P_E3
6	е	R₁₁=1, R₁₂=3, R₂₁=2, R₂₂=2, R₃=5, E₁₁=14, E₁₂=7, E₃₁=9, E₃₂=2	2,3	I₃, P_E31, P_R22
7	ж	R₂=2, R₃=3, R₄=4, R₅=5, J₁=0,1, J₆=0,5	4,5	I₂, P_J1, P_J6
8	з	R₂=1, R₃=5, R₄=4, R₅=3, E₆=28, J₁=0,9	2,6	I₄, P_J1, P_E6
9	и	R₁=2, R₂=4, R₃=4, R₄=2, R₅=6, E₁=12, J₆=0,4	1,3	I₃, U₅, P_R4
10	к	R₁=2, R₃=5, R₅=6, E₂=26, E₆=52, J₄=7	1,5	I₅, I₆, P_E6
11	л	R₂=2, R₃=1, R₄=4, R₅=5, E₁=13, E₆=26	1,4	I₂, U₅, P_E1
12	м	R₂=6, R₄=4, R₅₌5, R₆=1, J₁=2, J₃=5	4,6	U_J1, U₄, P_R6
13	н	R₁₁=3, R₁₂=1, R₂=2, R₃=2, R₄=2, R₅=4, E₁=19, E₅=38,	1,4	I₂, U₄, P_E5
14	о	R₂=1, R₃=2, R₄=5, R₅=4, J₁=7, J₆=21	4,5	I₃, U₂, P_J1
15	п	R₁=3, R₂=4, R₃=6, E₁=54, E₅=36, J₄=3,	1,2	I₁, U₃, P_R1
16	р	R₃=3, R₄=6, R₅=3, R₆=6, E₃=9, J₁=0,5, J₂=1,5	4,6	I₃, U₆, P_J2
17	с	R₁=1, R₃=4, R₅₁=3, R₅₂=2, E₁=10, J₂=0,2, J₄=0,4	1,3	I₁, U₂, P_E1
18	т	R₁=1, R₃=6, R₄₌3, R₆=5, E₇=16, J₂=0,5, J₅=0,2	4,6	I₆, U₃, P_R3
19	з	R₂=2, R₃=6, R₄₌3, R₅=4, E₆=16, J₁=0,4	2,3	I₄, U₂, P_J1
20	и	R₁=4, R₂=1, R₃₌2, R₄=3, R₅=3, E₁=56, J₆=4,5	3,4	I₅, U₄, P_E1
21	л	R₂=4, R₃=2, R₄=1, R₅=5, E₁=13, E₆=39	1,5	I₄, I₆, P_R2
22	н	R₁₁=1, R₁₂=2, R₂₌2, R₃=3, R₄=6, R₅=1, E₁=21, E₅=14,	4,5	I₅, U₅, P_E1
23	о	R₂=2, R₃=1, R₄=5, R₅=3, J₁=0,2, J₆=12	2,3	I₅, U₆, P_J6
24	т	R₁=4, R₃=6, R₄=3, R₆=2, E₇=16, J₂=0,5, J₅=0,3	3,7	I₇, U₆, P_R1
25	ж	R₂=2, R₃=3, R₄₌1, R₅=4, J₁=1, J₆=3	2,5	I₅, U₂, U₆