Приложение 4.
Решение уравнений состояния электрической цепи.
Основным методом решения уравнений
состояния является численный метод интегрирования с применением ЭВМ. В
вычислительной математике существует большой набор алгоритмов численного
решения систем дифференциальных уравнений, записанных в нормальной форме. В
машинных программах наибольшее распространение получил метод Рунге-Кутта
четвертого порядка с контролем точности вычислений на каждом шаге
интегрирования и регулировкой шага вычислений.
В
MATHCAD
программа интегрирования по методу Рунге-Кутта носит имя rkfixed. Обращение к
ней производится через операцию присваивания какой - либо переменной (здесь z)
имени программы:
z: = rkfixed(x, 0, tk, N, D),
где
x - вектор переменных состояния. Длина этого вектора - n задается
предварительным описанием вектора начальных значений и соответствует числу
уравнений состояния; 0 и tk - начало и конец временного интервала
интегрирования; N - число точек на интервале интегрирования; z - матрица
(массив), имеющая размер (N+1, n+1), где первый столбец (он же нулевой)
соответствует дискретным значениям времени ti: zi0 = i.
Остальные столбцы - совокупность значений
переменных состояния: zi1, zi2,…,
zin,
где индекс i изменяется от 1 до N; D - функция дифференцирования левой части
системы уравнений, которая описывает правую часть уравнений, разрешенных
относительно первых производных. Для линейных цепей эта функция имеет вид
линейного матричного преобразования D(t, x):=A·x+F, где A - квадратная
матрица коэффициентов, которые определяются структурой цепи и параметрами
элементов; F - вектор независимых переменных, параметры которого определяются
входными воздействиями, т.е. независимыми источниками питания цепи, которые
могут изменяться во времени.
Элементы матриц A и F должны быть
определены перед обращением к программе rkfixed. Для контроля правильности
задания исходных данных можно (но не обязательно) обратиться к программе
определения собственных чисел матрицы A: eigenvals(A). Эта программа выводит
информацию о собственных числах, которые совпадают с корнями
характеристического уравнения цепи. Необходимым (но недостаточным) условием
правильности ввода данных является набор отрицательных собственных чисел, или
комплексно-сопряженных с отрицательной вещественной частью.
Пример
1. Исследование переходного процесса в простейшей одноконтурной цепи
второго порядка, которая образуется после отключения источника постоянного
напряжения E от цепи. Эта задача рассмотрена в примере 3.5 для цепи (рис.
3.16а).
Параметры цепи: E = 40 В, r = 40 Ом, L = 1 Гн, C = 0,0005 Ф.
Начальные значения переменных: uC(0) = 40 B; iL(0) = 1 А.
Уравнения состояния цепи для переменных uC и iL имеют вид
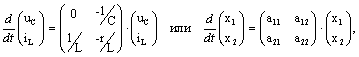
где x1 = zi1 = uC, x2 = zi2 = iL. Вектор
внешних источников питания F отсутствует.
Перед обращением к программе
интегрирования определяем (см.
распечатку) через операцию присваивания следующие величины:
1. Коэффициенты
матрицы
A: a11: = 0; a12: = -2000; a21: =
1; a22: = -40;
2.
Вектор начальных значений переменных x;
3. Число точек интегрирования N: = 500;
4. Формализованную матричную запись
уравнений состояния (здесь без вектора F):
D(t, x): = A·x;
5.
Правую границу временного интервала tk = 0,3 c.
Длительность участка интегрирования можно
оценить по собственным числам матрицы A путем обращения к программе
eigenvals(A). В этом примере имеем два комплексно-сопряженных числа p1 =
-20+j40 и p2 = -20-j40, вещественные части которых одинаковы и равны b=-20 1/c.
Эта часть комплексного числа определяет коэффициент затухания и непосредственно
связана с длительностью переходного процесса формулой: tk = 3/b.
В
рассматриваемом примере для наглядности интервал выбран в два раза
большим: tk = 6/b = 6/20 = 0, 3 с.
Далее следует обращение к самой программе интегрирования и
распе-чатка графика. Так как переменные состояния, измеряемые в разных единицах
- в вольтах и в амперах, могут численно значительно отличаться друг от друга,
то следует позаботиться о наглядности их графического изображения путем
введения соответствующих масштабных коэффи-циентов. Здесь для переменной zi2 =
x2 = iL
указан коэффициент 100. Чтобы получить истинное значение тока следует разделить
численные значения оси ординат на 100 для этой переменной.
В соответствии с характером собственных
чисел, переходный процесс носит колебательный характер, где обе переменные
постепенно затухают до нулевого значения.
Обращение к программе rkfixed
a11:=0 a12:=-2000 a21:=1 a22:=-40 tk:=0.3 N:=500
![]()
![]()
D(t,x):=A·x
z:=rkfixed(x,0,tk,N.D)
i:=0..N
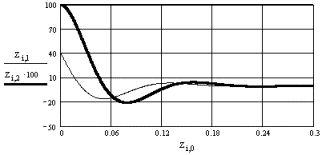
Пример
2. Исследование переходного процесса в цепи второго порядка, который
возникает после подключения к цепи (рис. 3.13) сопротивления r1. Эта задача
рассмотрена в примере 3.6, где были получены уравнения состояния цепи.
Параметры цепи: J = 2 А; r1 = r2
= 50 Ом; L = 5 мГн; С = 0, 1 мкФ.
Уравнения состояния для переменных x1 = zi1 = uC и x2=zi2=
iL
имеют вид
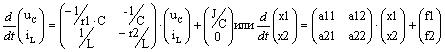 Значения коэффициентов можно вычислить заранее и включить в программу в
виде констант, или определить через операции присваивания в самой программе.
Значения коэффициентов можно вычислить заранее и включить в программу в
виде констант, или определить через операции присваивания в самой программе.
Значение N = 5000 указывается
произвольно и влияет только на время и точность вычислений. Точность вычислений
можно косвенно оценить, сравнив результаты интегрирования для двух значений N =
N1 и N = N1/2. Если результаты практически совпадают, то точность вычислений и
число точек интегрирования на интервале tk находятся в приемлемых пределах.
Через операцию присваивания определяются
также вектор исходных значений x и вектор независимых источников F.
Временной интервал tk может быть указан
произвольно или примерно определен параметрами цепи через анализ собственных
чисел матрицы A. Следует выбрать наименьшее по модулю собственное число pмин. и
воспользоваться формулой: tk = 3/pмин. В данном примере имеем p1 = -1, 888E5
1/c и p2 = -2, 118E4 1/с. Следовательно, tk = 3/2, 118E4 = 1, 42E-4 c.
Другой способ определения tk основан на
анализе постоянных времени цепей первого порядка, которые можно построить на
основе исходной цепи путем последовательного исключения реактивных элементов.
Каждая такая цепь содержит один реактивный элемент, и для нее длительность
переходного процесса определяется формулой tk=3·C·R , если это RC цепь, и
tk=3·L/R если это LR цепь, где R - входное резистивное сопротивление цепи со
стороны реактивности. Исключение индуктивности соответствует замене ее на
короткозамкнутую перемычку, исключение емкости соответствует разрыву ветви, в
которой стоит емкость. В данном примере имеем t0 = 3·L/(r1+r2) и
t1=3·C·r1·r2/(r1+r2). Осуществляется процедура выбора из этих чисел
наибольшего: tk: = max(t). Здесь это число равно tk = 1, 5E-4, что практически
совпадает с ранее полученным значением.
Формализованная матричная запись
уравнения состояния определена в самой общей форме с учетом вектора внешних
воздействий: D(t, x)=A·x+F.
Распечатка графиков произведена с учетом введения масштабного
коэффициента 100 для переменной zi2 = iL. Переходный процесс
носит апериодический характер. Напряжение на емкости изменяется от уровня uC(0-) = 100 B до уровня
uCпр. = 50 В. Ток в индуктивности изменяется от значения iL(0-)=2 А до
значения iLпр. = 1 А. Можно отметить в решении точки экстремума и
перегиба функций.
Обращение к программе rkfixed
J:=2 r1:=50 r2:=50 L:=5·10-3
C:=1·10-7 N:=5000
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
D(t,
x):=A·x+F ![]() tk:=max(t)
tk:=max(t)
tk=1.5![]() 10-4
10-4
z:=rkfixed(x,
0, tk, N, D)
i:=0..N
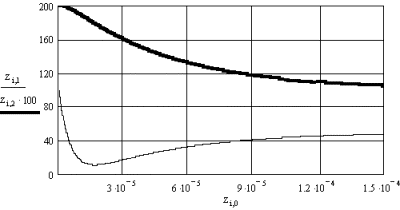
Пример
3. Исследование переходного процесса в цепи третьего порядка (рис. 3.23),
который возникает после подключения к цепи сопротивления r5. Переходный процесс
обеспечивается независимым источником напряжения Е, а также энергией
электромагнитного поля, запасенной
в индуктивностях L1
и L2 и емкости C.
Параметры цепи:
Е
= 120 В; r1 = r3 = r4 = 1 Ом; r2 = 2 Ом; r5 = 2 Ом; L1 = 1 мГн; L2 = 2 мГн;
C=10
мкФ. Уравнения состояния цепи для этой задачи получены в примере 3.7.
Переменными состояния будут x1=zi1=uC, x2=zi2=iL1 и x3=zi3=iL2. Система уравнений в
данном случае имеет вид
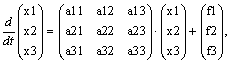
где
определена промежуточная переменная g:=1/(r3+r4+r5), а также сами коэффициенты
aij: a11:=-g/C; a12:=g·(r4+r5)/C; a13:=-g·r5/C; a21:=-g·(r4+r5)/L1; a22:=-g·(r1·r5+r3·r4+r3·r5+r1·r3+r1·r4)/L1;
a23:=g·r3·r5/L1; a31:=g·r5/L2;
a32:=g·r3·r5/L2;
a33:=-(r2+(r3+r4)·r5·g)/L2.
Параметры вектора независимых
источников: f1: = 0; f2: = E/L1; f3: =0.
Вектор начальных значений переменных
может быть введен в виде формул или числами x:= (90 30 30)T.
Вывод информации о собственных числах
матрицы A позволяет судить о характере переходного процесса; он апериодический,
так как собственные числа все вещественные и отрицательные. По этим числам
выбирается время переходного процесса как утроенное значение обратной величины
от наименьшего по модулю собственного числа: tk: = 3/(min(li)). В
рассматриваемом примере это число l3 = 1, 268E3. Тогда tk = 2E-3 c.
Остальные операторы и обращение к
программе интегрирования такое же, как и в рассмотренных ранее примерах.
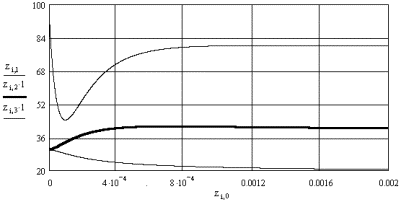
Обращение к программе rkfixed
E:=120 r1:=1 r2:=2 r3:=1 r4:=1
r5:=2 L1:=1·10-3 L2:=2·10-3 C:=1·10-5 N:=5000
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
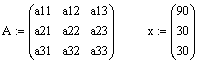
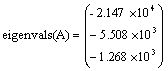
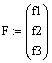 D(t,
x):=A·x+F
D(t,
x):=A·x+F ![]()
![]()
tk:=2.366·10-3
z:=rkfixed(x,
0, tk, N, D)
i:=0..N