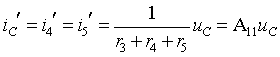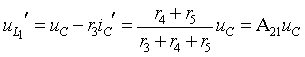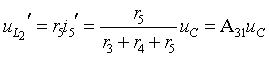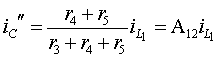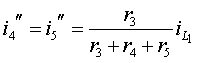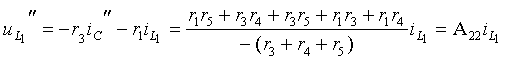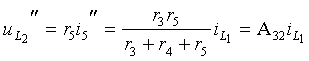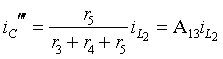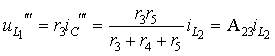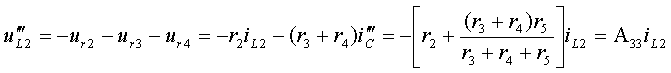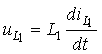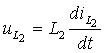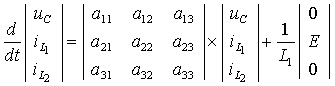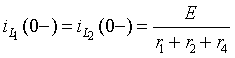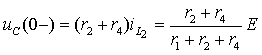3.4.2 Использование метода наложения

 

     Резистивная схема замещения цепи, содержащая значительное число источников разных типов с трудом поддается анализу, так как не всегда бывает возможным отделить влияние на переменную состояния одного источника от другого. Использование фундаментальных методов расчета цепей - метода контурных токов или метода узловых потенциалов уводит решение задачи в сторону, так как в этих методах находятся не переменные состояния, а токи или потенциалы узловых точек. На самом деле необходимо установить степень влияния данного источника энергии на каждую переменную состояния. В силу того, что в линейной электрической цепи источники энергии действуют независимо друг от друга, для оценки этого влияния целесообразно использовать метод наложения.

     Рассматривая действие какого-либо источника на цепь, нужно оставить в цепи этот источник, а другие источники исключить, заменив их внутренними сопротивлениями: источники напряжения (ЭДС) заменить короткозамкнутыми перемычками (режим короткого замыкания - к.з.), а источники тока разорвать (режим холостого хода - х.х.). В этом случае схема цепи значительно упрощается, и есть возможность определить долю влияния оставленного в цепи источника энергии на все исследуемые производные от переменных состояния. На заключительной стадии анализа цепи суммируются частные решения с учетом знаков и формируются уравнения состояния.

 

     Пример 3.7 Сформировать уравнения состояния для цепи рис.3.23а. Цепь третьего порядка питается от источника постоянного напряжения, ключ S замыкается.

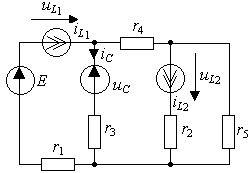
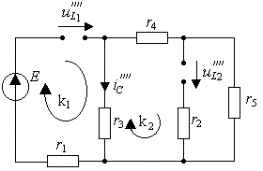
     На рис.3.23б изображена резистивная схема замещения цепи, где все реактивные элементы заменены источниками тока и напряжения. Положительные направления токов и напряжений источников согласованы с исходной цепью. В цепи подлежат определению емкостной ток и напряжения на источниках тока  и ,так как именно они определяют производные от переменных состояния. В соответствии с принципом наложения рассмотрим четыре схемы (по числу источников), где действуют поочередно каждый из источников энергии.

                                     

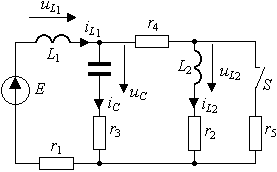
                                                   а)                                                                                  б)

Рис. 3.23. Схема L1,L2,C,R–цепи третьего порядка:

а)  исходная схема

б) эквивалентная схема замещения цепи (t>0)

 

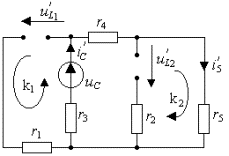
     а) Действие источника  показано на рис.3.24а, остальные источники заменены их внутренними сопротивлениями.

                  

                                                     а)                                                                         б)

Рис. 3.24. Схема для определения влияния переменных состояния на их производные:

а)  анализ переменной uC

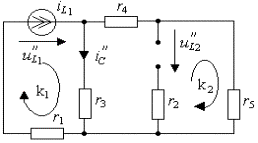
б)  анализ переменной

 

     Здесь существует только один контур, где протекает электрический ток     

     Напряжения на источниках тока (индуктивностях) найдем из контуров k1 и k2:

     б) Действие источника тока  показано на рис.3.24б, остальные источники заменены внутренними сопротивлениями.

     По правилу деления тока на части найдем токи          

     Напряжения на источниках тока найдем из контуров k1 и k2:

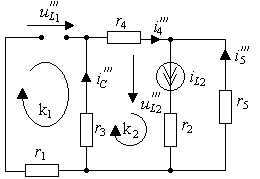
     в) Действие источника тока  показано на рис.3.25а.

                

                                                         а)                                                                             б)

Рис.3.25. Схема для определения влияния переменных состояния на их производные:

а)  анализ переменной

б) анализ переменной E

 

     Используя правило деления тока на части, найдем ток в емкости

     Для контура k1 найдем напряжение  

     Из контура k2 найдем напряжение на источнике тока

     г) Действие независимого источника напряжения E показано на рис.3.25.б.

     Остальные источники заменены внутренними сопротивлениями. Так как в ветви с источником E есть разрыв, все токи в ветвях равны нулю:

     Из контура k найдем напряжение . Очевидно, что .

     После решения последней частной задачи следует объединить слагаемые с учетом знака (выбранных положительных направлений токов и напряжений).

    Если параметры цепи заданы, то коэффициенты  принимают численные значения. С учетом компонентных соотношений

перепишем систему уравнений в форме Коши, т.е. окончательно сформируем нормальную систему дифференциальных уравнений для переменных состояния и запишем ее в матричной форме          

(3.31)

 

где   ;     ;     ;

        ;     ;    ;  

        ;      ;     

     К системе уравнений, записанной в нормальной форме, следует добавить вектор, который отражает состояние цепи в начале переходного процесса, т.е. в момент времени t=0. Так как переменные состояния подчиняются законам коммутации, то этот вектор может быть получен из анализа докоммутационного состояния цепи. Для рассматриваемого примера эта схема имеет вид, представленный на рис.3.26.

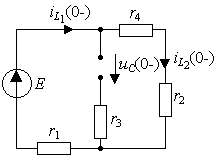
                                   Рис.3.26. Схема для анализа цепи до коммутации

 

     По контуру k протекает постоянный ток, он и будет равен токам в индуктивностях:

     Напряжение на емкости определяется напряжением на параллельной ветви:

    Вектор  отражает начальное состояние цепи и необходим для осуществления начала интегрирования системы дифференциальных уравнений.

     Задача решена.

 

     Результат процесса интегрирования уравнений (3.31) на ПЭВМ приведен в Приложении 4 (см. пример 3).

 

     Токи и напряжения других ветвей можно найти путем решения обратной задачи через использование переменных состояния, как это было рассмотрено выше в примерах 3.1, 3.2, 3.4. Если решение задачи выполняется с помощью ЭВМ, то определение дополнительных переменных следует организовать в том же цикле расчета переменных состояния.

к содержанию