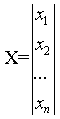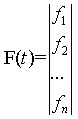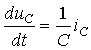3.4 Уравнения
состояния электрической цепи
Для электрических цепей более высокого
порядка (n > 2), включающих
емкостей и 
индуктивностей,
переходные процессы исследуются путем составления и решения системы уравнений
состояния. При этом предполагается, что цепь состоит из набора канонических
ветвей и имеет место независимость всех переменных состояния друг от друга. Как
было отмечено ранее, под переменными состояния понимают напряжения на емкостях 
и токи в
индуктивностях 
. Общий путь расчета в этом методе основан на составлении 
дифференциальных
уравнений первого порядка относительно переменных состояния 
, записанных в нормальной форме Коши
|
|
|
Коэффициенты в правых частях уравнений
состояния 
определяются
структурой цепи и параметрами ее элементов, а функции 
учитывают влияние внешних независимых источников энергии на
скорость изменения каждой переменной состояния. Переменные состояния однозначно
определяют запас энергии цепи в любой момент времени, а, следовательно, через
эти переменные однозначно определяются остальные токи и напряжения.
Для линейных цепей система уравнений
состояния также линейна, и ее обычно записывают в матричной форме
|
|
(3.30) |
где X - вектор
переменных состояния; A - квадратная
матрица; F(t) - вектор входных воздействий.
|
|
|
|
Эта система полностью определяет
поведение цепи в переходном режиме. Формирование системы уравнений (3.30)
основано на известных дифференциальных соотношениях (3.21), из которых
непосредственно записываются производные от переменных состояния
|
|
|
Если выразить правые части этих
соотношений как функции всех переменных состояния и внешних источников
воздействий, то это позволит сформировать систему уравнений (3.30). Для этой
цели можно использовать законы Кирхгофа или метод наложения.