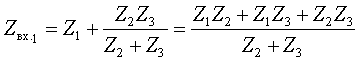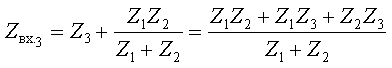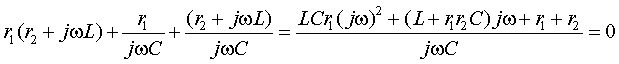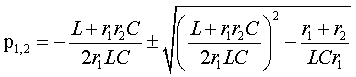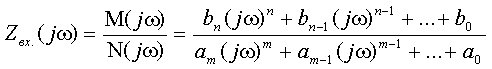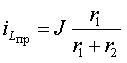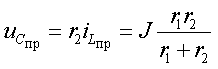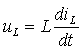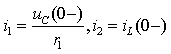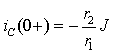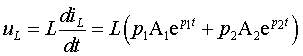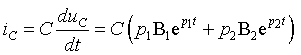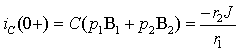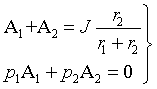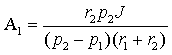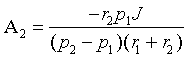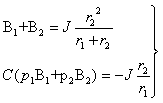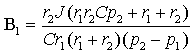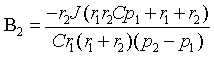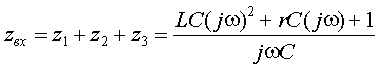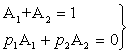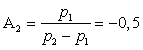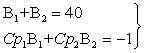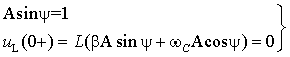3.3 Переходные процессы в цепях второго порядка

Цепи второго порядка содержат два реактивных элемента; это могут быть две индуктивности, две емкости или емкость с индуктивностью. Кроме того, цепь включает некоторое количество резистивных элементов и независимых источников энергии, которые для простоты анализа будем считать стационарными. В зависимости от наличия тех или иных реактивных элементов, решение задачи следует искать или для переменной состояния i_L(t), или для u_C(t). Форма записи решения определена общей теорией:

(3.17)

(3.18)

где p₁ и p₂ - корни характеристического уравнения.

Поиск решения выполняется в той же последовательности, что и для цепей первого порядка:

1. Находят корни характеристического уравнения. Они могут быть вещественными разными и отрицательными или вещественными кратными и отрицательными или комплексно-сопряженными с отрицательной вещественной частью;

2. Из анализа цепи после коммутации определяют принужденную составляющую режима или , что можно сделать, если в цепи продолжают действовать стационарные источники питания;

3. Исследуя основные и неосновные начальные условия, находят постоянные интегрирования , или, .

Рассмотрим подробнее каждый шаг решения.

1. Определение корней характеристического уравнения.

Характеристическое уравнение может быть получено классическим методом путем составления системы уравнений по законам Кирхгофа с последующим сведением этой системы к одному дифференциальному уравнению второго порядка. Этот способ подробно описан в учебной литературе и здесь не рассматривается. Как показывают примеры, рассмотренные ранее, этот путь сопровождается достаточно громоздкими преобразованиями.

Было замечено, что характеристическое уравнение содержится внутри

функции входного сопротивления как некоторый инвариант, присущий данной цепи. Рассмотрим этот способ получения характеристического уравнения путем исследования входного сопротивления на примере цепи, представленной на рис.3.13а. Будем считать, что цепь питается от источника постоянного тока и содержит два резистивных сопротивления, индуктивность и емкость. После коммутации (t>0) (ключ S замыкается) переходный процесс в цепи, изображенной на рис.3.13б, развивается за счет независимого источника тока, а также за счет энергии, запасенной в реактивных элементах цепи. Свободная составляющая режима, определяемая корнями характеристического уравнения, не зависит от внешнего источника питания, а определяется только параметрами элементов ветвей и способом их соединения. Точно так же не зависит от внешних источников питания и функция входного сопротивления [1]. Поэтому возникает идея поискать корни характеристического уравнения внутри функции входного сопротивления.

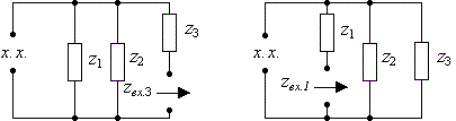
На рис.3.13в и рис.3.13г представлены комплексные схемы замещения цепи, которые следует составить для определения входного сопротивления со стороны

первой и третьей ветви, где .

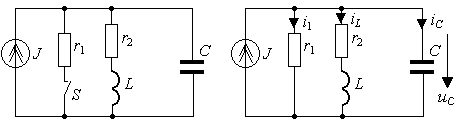
а) б)

в) г)

Рис. 3.13. Схема RLC-цепи второго порядка:

а) исходная цепь

б) схема после коммутации

в) входное сопротивление со стороны третьей ветви

г) входное сопротивление со стороны первой ветви

Объединяя параллельно и последовательно соединенные ветви, найдем входные сопротивления со стороны обозначенных зажимов

Числители полученных выражений совпадают, а знаменатели различны. Аналогичный результат получим, если найдем входное сопротивление со стороны второй ветви. Следовательно, числитель входного сопротивления со стороны любой ветви является некоторым расчетным инвариантом, определяемым топологией цепи. Числитель этого инварианта при замене комплексной переменной jω на p совпадает с характеристическим полиномом. Используя эту замену и, приравнивая числитель к нулю, получим характеристическое уравнение:

или

После замены в числителе переменной jω на p и деления на коэффициент при старшем члене получим уравнение второй степенин.Найдем корни этого уравнения

На основании этого анализа сформулируем порядок получения характеристического уравнения цепи:

а. Для времени t>0 следует изобразить комплексную расчетную цепь;

б. Исключить из схемы все независимые источники энергии: источники тока разомкнуть, источники напряжения замкнуть накоротко. Найти входное сопротивление со стороны любой ветви и записать это выражение в виде дробно-рациональной функции, где в числителе и в знаменателе образуются полиномы по степеням jω

в. Числитель полученного выражения, совпадающий с характеристи-ческим полиномом, приравнять к нулю, предварительно заменив переменную jω на p. Найти корни характеристического уравнения и записать решение для искомой переменной состояния в виде (3.17) или (3.18).

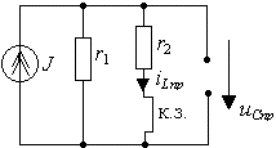
Рис. 3.14. Схема для определения принужденных составляющих режима

2. Определение принужденной составляющей режима при стационарном воздействии находят для момента времени t = ∞, когда переходный процесс в цепи уже закончен. Для рассматриваемого в примере режима постоянного тока исследуемая схема приведена на рис.3.14, где индуктивность заменена короткозамкнутой перемычкой, а емкость разрывом. Используя правило деления тока на части, найдем

3. Постоянные интегрирования A₁ и A₂ (или B₁ и B₂) можно найти на основании основных и неосновных начальных условий. Основные начальные условия определяются законами коммутации по схеме докоммутационного состояния цепи. Для рассматриваемого примера такая схема приведена на рис.3.15а, из анализа которой следует

что дает одно уравнение для определения постоянных интегрирования:

(3.19)

или

(3.20)

Второе уравнение получим из анализа неосновных начальных условий, которые определяются исследованием энергетического состояния цепи для момента времени t = 0+. К этим условиям относят численные значения напряжений на индуктивностях и токов в емкостях в первый момент после коммутации, которые претерпевают скачок в момент коммутации и связаны с переменными состояния известными дифференциальными соотношениями:

(3.21)

Для рассматриваемого примера анализируемая схема цепи представлена на рис.3.15б. Особенностью этой цепи по сравнению с исходной является появление двух новых внутренних источников энергии, которые обусловлены законами коммутации и перешли в анализируемую схему из предыдущей схемы рис.3.15а. Фактически исследуется цепь постоянного тока, содержащая резистивные элементы, а также внешние и внутренние источники энергии. Расчет цепи может выполняться любым методом. Целесообразно, например, использовать законы Кирхгофа или метод наложения.

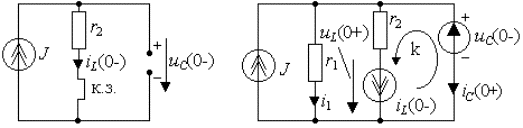
а) б)

Рис. 3.15. Схема для анализа состояния цепи:

а) до коммутации

б) в первый момент после коммутации

Составим уравнение равновесия напряжений для контура k, который включает искомое напряжение на источнике тока . Ток в сопротивлении определен этим источником, поэтому напряжение u_L(0+) находится сразу

После подстановки найденных ранее значений получим .

На основании первого закона Кирхгофа, найдем ток в емкости :

где

После подстановки в уравнение равновесия получим

Используя общий вид решения (3.17) и (3.18), найдем

(3.22)

(3.23)

Для исследуемого момента времени t = 0+ имеем равенства

(3.24)

(3.25)

Объединяя уравнения (3.19) и (3.24) в систему, найдем постоянные интегрирования A₁ и A₂

Подстановка значений A₁ и A₂ в выражения (3.17) и (3.22) позволяет окончательно записать ток и напряжение в индуктивности. Другие токи и напряжения могут быть найдены путем решения обратной задачи:

1.Напряжение на втором резистивном элементе:

2.Напряжение на емкости:

3.Ток в емкости:

4.Ток в первом резистивном элементе:

Решение задачи через определение переменной состояния на этом можно считать законченным.

Второй путь решения заключается в первоначальном определении напряжения на емкости, что предполагает нахождение постоянных интегрирования B₁ и B₂ . Это можно осуществить, объединив в систему уравнения (3.20) и (3.25):

Решение системы:

Подставив постоянные интегрирования B₁ и B₂ в выражения (3.18) и (3.23), окончательно найдем напряжение и ток в емкости.

Решением обратной задачи определим:

1 .Ток в первом резистивном элементе:

2. Ток в индуктивности:

3.Напряжение на индуктивности:

4.Напряжение на втором резистивном элементе:

Задача решена.

Пример 3.4. Исследовать переходный процесс в цепи рис.3.16а после размыкания ключа S. Параметры цепи: E = 40 B, r = 40 Ом, L = 1 Гн, С = 1/300 Ф.

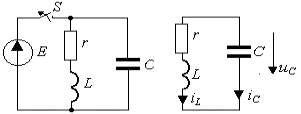
а) б)

Рис. 3.16. Схема простейшей RLC–цепи второго порядка:

а) до коммутации

б) в первый момент после коммутации

После размыкания ключа источник питания E отсоединяется от цепи и в переходном процессе не участвует. Процесс развивается только за счет энергии электрического и магнитного поля, накопленной к моменту коммутации в реактивных элементах.

1. Для момента времени t>0 (см. рис.3.16б) найдем входное сопротивление одноконтурной цепи, заменив элементы на комплексные сопротивления , , .

После замены на p приравниваем нулю числитель и находим корни характеристического уравнения

Соответственно определим две постоянные времени как величины, обратные коэффициентам затухания

В дальнейшем можно определять либо ток в индуктивности, либо напряжение на емкости.

Запишем свободную составляющую режима для тока в индуктивности

(3.26)

2. Принужденная составляющая режима, которая находится для момента времени , дает в этом примере нулевое значение, так как после окончания переходного процесса вся энергия, запасенная в реактивных элементах, преобразуется в тепловую энергию в резистивном элементе. Имеем, i_Lпр = 0 ; .

3. Объединяя свободную и принужденную составляющую, найдем

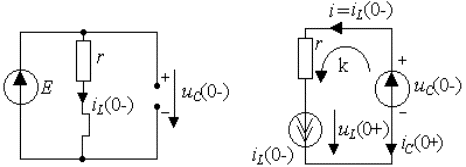
4.Анализ основных и неосновных начальных условий позволяет определить постоянные интегрирования. Найдем эти условия из анализа цепей, представленных на рис.3.17аб. Для первой цепи (t<0) находятся основные начальные условия

а) б)

Рис. 3.17. Схема для определения состояния цепи:

а) до коммутации

б) в первый момент после коммутации

Для второй цепи (t = 0+) определим неосновные начальные условия, где основные начальные условия перенесены из первой цепи в виде источников напряжения и тока. Из уравнения равновесия для напряжений имеем

т.е.

Рассматривая выражения (3.26) и (3.22) для момента времени t = 0, сформируем систему уравнений, из которой найдем постоянные интегрирования

Окончательно запишем , или i_L= i_L1+i_L2, где , а .

График найденной функции тока показан на рис.3.18. Переходный режим носит апериодический характер, так как корни характеристического уравнения получились вещественными и отрицательными. Коэффициент затухания второй экспоненты в три раза больше, чем первой, и она быстро затухает в пределах , а переходный процесс для t > в основном определяется первой экспонентой.

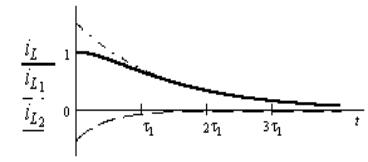
Рис. 3.18. График апериодического переходного процесса

Используя найденное решение для тока в индуктивности, определим:

1. Напряжение на индуктивности по формуле (3.22):

2. Напряжение на резистивном элементе:

3. Напряжение на емкости:

Решение задачи путем использования переменной состояния можно считать законченным.

Рассмотрим другой путь решения той же задачи через определение напряжения на емкости. Форма записи решения остается прежней:

(3.27)

Неосновным начальным условием здесь является значение тока в емкости в первый момент после коммутации. Найдем его из цепи рис.3.17б.

Рассматривая выражения (3.27) и (3.23) для момента времени t = 0, составим систему уравнений, из которой найдем постоянные интегрирования

На основании (3.27) окончательно запишем ответ, который совпадает с ранее полученным выражением

Решение задачи путем использования переменной состояния можно считать законченным.

Характер переходного процесса меняется на колебательный с увеличением влияния реактивных параметров цепи, что обеспечивается увеличением L или уменьшением C. Если в рассматриваемом примере уменьшить значение емкости до величины С = 0,0005 Ф при сохранении величин других параметров, то корни характеристического уравнения станут комплексно-сопряженными

p2 = b - jwC = -20 - j40

где выполняет роль коэффициента затухания, а- угловой частоты собственных колебаний контура. В случае появления комплексно-сопряженных корней решение для тока следует записать в виде

(3.28)

где A и выполняют роль постоянных интегрирования. Напряжение на индуктивности также изменяет свою форму записи

(3.29)

Используя основные и неосновные начальные условия а также выражения (3.28) и (3.29), составим систему уравнений для определения постоянных A и

Из второго уравнения найдем ,откуда ,или рад. Далее из первого уравнения получим A = 1,117. Запишем окончательно решение

Для построения графика в зависимости от обобщенной переменной , измеряемой в радианах, следует привести к той же переменной начальную фазу и показатель степени у экспоненты путем подстановки

:

График этой зависимости приведен на рис.3.19. Переходный процесс напоминает затухающую синусоиду, смещенную влево так, что значение тока в нулевой момент времени обеспечивает в соответствии с законом коммутации величину, равную одному амперу. Синусоида изменяется в границах двух функций и.

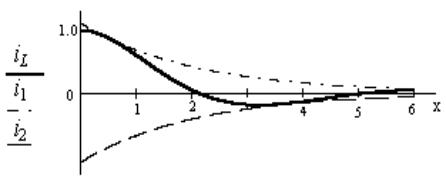
Рис. 3.19. График колебательного затухающего процесса

Задача решена.

к содержанию