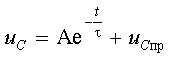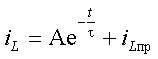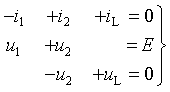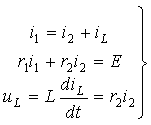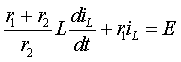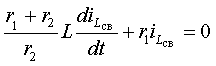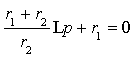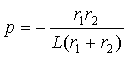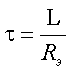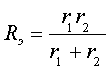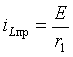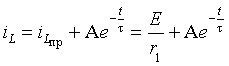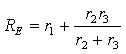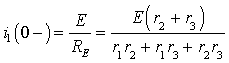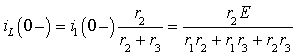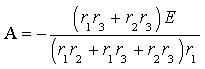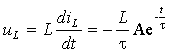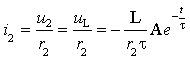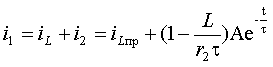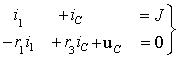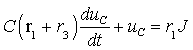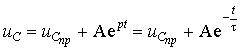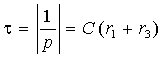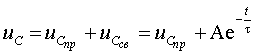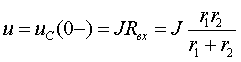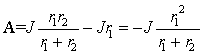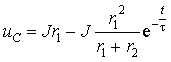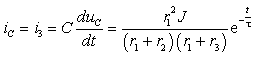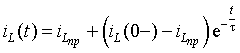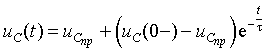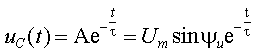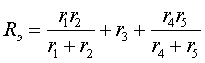3.2 Электрические цепи первого порядка

Порядок электрической цепи определяется числом реактивных элементов. Цепь первого порядка (n = 1) включает один реактивный элемент - индуктивность или емкость и любое число резистивных элементов и независимых источников питания. По отношению к реактивному элементу всю остальную цепь можно считать резистивным активным двухполюсником (рис. 3.1а,б).

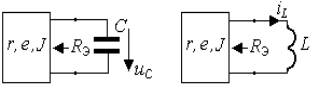
а) б)

Рис. 3.1. Схематичное изображение цепи первого порядка:

а) RC-цепь; б) RL-цепь

Переходный процесс в такой цепи описывается дифференциальным уравнением первого порядка, решение которого для переменных состояния или будет иметь вид

где p - корень характеристического уравнения. Эта величина вещественна и отрицательна, она выполняет роль коэффициента затухания. Обратное отношение , измеряемое в секундах, определяет скорость переходного процесса и называется постоянной времени. Принято считать длительностью переходного процесса величину равную . C учетом этого определения решение чаще всего записывают в виде

или

(3.10)

Итак, для того чтобы получить решение для переменных состояния или , достаточно в выражениях (3.10) найти три значения:

1. Постоянную времени τ для свободной составляющей режима;

2. Принужденную составляющую - или ;

3. Постоянную интегрирования A.

Рассмотрим эту триединую задачу на примерах.

Пример 3.1. В цепи рис. 3.2а, которая питается от источника постоянного напряжения E, происходит замыкание ключа S. Найти закон изменения тока в индуктивности.

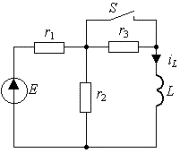
а) б)

Рис. 3.2. Схема RL-цепи первого порядка:

а) исходная цепь(t<0); б) схема после коммутации(t>0)

Предварительный анализ цепи показывает, что в процессе коммутации сопротивление замыкается накоротко и не участвует в переходном процессе, а сам процесс развивается за счет внешнего источника энергии E и энергии магнитного поля, запасенной в индуктивности к моменту коммутации. На рис.3.2б представлена измененная схема цепи после замыкания ключа.

В соответствии с требованием классического метода для времени t>0 составим систему уравнений по законам Кирхгофа [1]

После подстановки компонентных соотношений, связывающих токи и напряжения в отдельных элементах цепи, получим

Подставим первое и третье уравнение во второе, чем сведем систему

к одному уравнению относительно переменной состояния :

Уравнение для свободной составляющей режима получим, приравняв правую часть к нулю

Переход к характеристическому уравнению произведем заменой d/dt на p, а на 1 :

Найдем корень характеристического уравнения, модуль которого совпадает с коэффициентом затухания

Постоянную времени получим как величину обратную коэффициенту затухания

(3.11)

где

(3.12)

Анализ выражений (3.11) и (3.12) показывает, что постоянная времени, пропорциональна величине индуктивности L и обратно пропорциональна некоторому эквивалентному резистивному сопротивлению. Величина совпадает с входным сопротивлением исследуемой цепи, измеряемым или вычисляемым со стороны реактивного элемента [1].Этот вывод распространяется на любую цепь первого порядка, содержащую одну индуктивность и неограниченное число резистивных элементов и источников энергии. Таким образом, для получения конечного выражения (3.11) не обязательно составлять и решать систему алгебраических и дифференциальных уравнений. Достаточно найти входное сопротивление цепи со стороны реактивного элемента, а затем воспользоваться формулой (3.11).

Входное сопротивление цепи определяется в три этапа:

а. Изображается схема цепи после коммутации (t>0);

б. В этой цепи вместо реактивного элемента рисуют разомкнутые зажимы, по отношению к которым в дальнейшем определяют входное сопротивление. Далее исключают все источники энергии: источники напряжения замыкают накоротко, а источники тока разрывают;

в. Последовательно упрощают цепь, объединяя последовательно и параллельно соединенные резистивные элементы, чем сводят цепь к эквивалентному сопротивлению, которое и будет искомым входным .

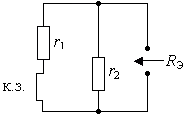
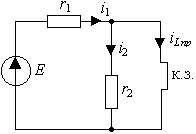
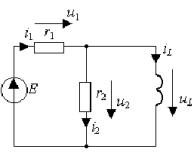
Рис. 3.3. Схема для определения Рис. 3.4. Схема для определения

входного сопротивления активного принужденной составляющей

двухполюсника режима

Для рассматриваемой цепи такая преобразованная схема показана на рис.3.3. Здесь вместо индуктивности изображены разомкнутые зажимы, со стороны которых требуется определить входное сопротивление, а вместо источника напряжения E показана короткозамкнутая перемычка. Сопротивления и , участвующие в переходном процессе, оказываются соединенными параллельно, и их эквивалентная замена совпадает в выражением (3.12), что и подтверждает вышесказанное.

2. Принужденную составляющую решения определим для бесконечно большого момента времени (t=), когда переходный процесс закончен и цепь находится под воздействием стационарного постоянного источника питания E. Целесообразно для этого режима нарисовать расчетную схему. Если в цепи есть индуктивность, то она заменяется короткозамкнутой перемычкой, так как сопротивление индуктивности постоянному току равно нулю. Эта схема изображена на рис.3.4.Очевидно, что ток в индуктивности ограничен только сопротивлением :

Используя выражение (3.7), сформируем решение в виде суммы свободной и принужденной составляющей:

3. Постоянную интегрирования A определим на основании первого за-

кона коммутации (3.1).Для момента времени t = 0 имеем ,

или.

Отсюда следует общая формула определения постоянной интегрирования для цепей первого порядка, включающих одну индуктивность:

(3.13)

Для определения нужно найти токи в цепи до коммутации (t=0-). Исследуемая цепь представлена на рис. 3.5, в которой требуется определить ток i_L (0-). Снова решается задача расчета цепи постоянного тока, где индуктивность заменена короткозамкнутой перемычкой. Для решения могут быть использованы все методы расчета цепей постоянного тока, включая законы Кирхгофа и эквивалентные преобразования.

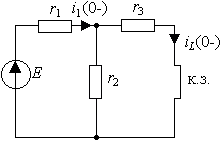
Рис. 3.5. Схема для анализа докоммутационного состояния цепи

Так как исследуемая цепь включает один источник энергии, то наиболее просто получить результат можно путем использования метода эквивалентных преобразований, вычисляя входное сопротивление цепи со стороны источника напряжения

Тогда ток

Искомый ток является частью тока и определяется правилом деления тока на части:

По формуле (3.13) окончательно определим постоянную интегрирования

График функции тока схематично изображен на рис.3.6а. За время ток почти приближается к установившемуся значению, и это время считается длительностью переходного процесса.

Найденное выражение для переменной состояния позволяет определить все токи и напряжения. Для этого следует, опираясь на известную переменную состояния, решить обратную задачу: последовательно шаг за шагом, используя законы Ома и Кирхгофа, а также компонентные соотношения, определить токи и напряжения в других ветвях [1]. Для рассматриваемого примера найдем:

а. Напряжение на индуктивности:

б. Ток:

в. Ток:

г. Напряжение:

Все найденные как следствие функции имеют разрыв в точке t = 0.

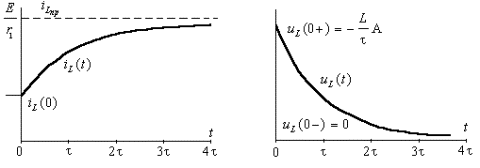
а) б)

Рис. 3.6. Графики переходного процесса: а)ток в индуктивности; б)напряжение на индуктивности

Например, график функции , изображенный на рис.3.6б, претерпевает скачок от нулевого значения до уровня -L(A - отрицательно), а затем плавно уменьшается до нулевого значения. Это означает, что, как правило, для функций, которые не являются переменными состояния, законы коммутации не выполняются, и, следовательно, определение для них постоянных интегрирования встречает дополнительные трудности. Если сразу искать выражения для этих функций, то требуется провести дополнительное исследование состояния цепи для момента времени t = 0+. Предложенный в этом пособии путь решения задачи через переменные состояния является наиболее оптимальным, так как требует знания только основных начальных условий, определяемых законами коммутации.

Задача решена.

Пример 3.2. В цепи рис.3.7а найти закон изменения напряжения на емкости после размыкания ключа S, если цепь питается от источника постоянного тока J = const.

Предварительный анализ цепи показывает, что до размыкания ключа S ток источника протекал по параллельно соединенным сопротивлениям и , при этом емкость была заряжена до некоторого напряжения . После размыкания ключа сопротивление уже не участвует в переходном процессе, и структура цепи принимает вид рис.3.7б. В измененной цепи переходный процесс возникает за счет действия независимого источника энергии J и энергии, запасенной в емкости к моменту коммутации, в результате чего напряжение на емкости приходит к новому установившемуся состоянию.

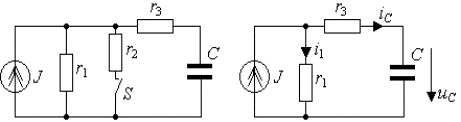
а) б)

Рис. 3.7. Схема RC-цепи первого порядка:

а) исходная цепь (t<0); б) схема после коммутации (t>0)

1. Составим систему уравнений цепи по законам Кирхгофа:

где переменной состояния для этой цепи будет напряжение . С учетом компонентного соотношения сведем систему уравнений к одному уравнению относительно переменной u_C

Как и следовало ожидать, переходный процесс описывается неоднородным дифференциальным уравнением первого порядка. Решение его имеет вид

Приравнивая нулю правую часть уравнения и делая замену на p, а также на 1, получим характеристическое уравнение

откуда определяется единственный корень .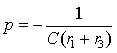

Постоянную времени цепи определим как модуль обратной величины от коэффициента затухания

Полученный результат, запишем в более общей форме

(3.14)

где ; т.е. постоянная времени для цепи первого порядка с одной емкостью вычисляется как произведение емкости С и некоторого эквивалентного сопротивления . Это эквивалентное сопротивление находится как входное сопротивление цепи со стороны реактивности (здесь емкости). На рис.3.8 показана эта схема, которая построена на основе исходной цепи рис.3.7б путем исключения источника энергии - заменой его на разомкнутые зажимы, а также обозначением разомкнутых зажимов вместо емкостного элемента. По отношению к обозначенным зажимам сопротивления и соединены последовательно, следовательно, , что совпадает с ранее полученным решением.

Второй способ определения быстрее приводит к поиску свободной составляющей режима, чем составление и решение системы уравнений.

2. Принужденную составляющую режима определим для бесконечно большого момента времени , когда переходный процесс уже закончен, и цепь находится в новом энергетическом состоянии. Для этого момента времени схема цепи изображена на рис.3.9, где емкость С заменена разрывом ветви, поскольку сопротивление емкости постоянному току бесконечно большое. Следовательно, и , а из контура k имеем уравнение равновесия для напряжений:

откуда найдем

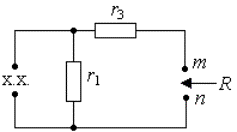
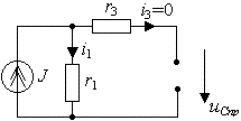
Рис. 3.8. Схема для определения Рис. 3.9. Схема для анализа

входного сопротивления принужденных составляющих

активного двухполюсника режима

Объединяя свободную и принужденную составляющую режима, получим:

(3.15)

3. Постоянную интегрирования A для выражения (3.15) найдем на основе второго закона коммутации (3.4):

(3.16)

Формула (3.16) имеет общий характер и ей можно пользоваться для цепей первого порядка при наличии емкостного элемента. Для определения следует рассмотреть состояние цепи до коммутации (см. рис.3.10).

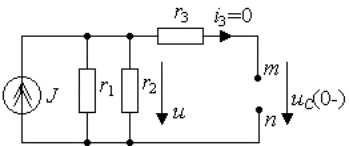
Рис. 3.10. Схема для анализа докоммутационного состояния цепи

Аналогично пункту 2 ток источника тока J создает падение напряжения на параллельно соединенных сопротивлениях и

Это же напряжение приложено к разомкнутым зажимам m, n. Используя формулу (3.16), окончательно получим

График переходного процесса для переменной представлен на рис.3.11.

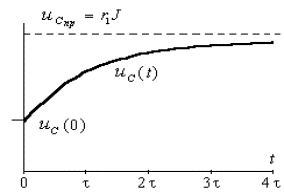
Рис.3.11. График переходного процесса напряжения на емкости

Как следствие решенной задачи можно найти токи и напряжения в других элементах цепи:

а. Ток в емкости и в резистивном сопротивлении r₃

б. Напряжение на сопротивлении:

в. Напряжение на сопротивлениях и :

г. Токи в сопротивлениях и :

Все эти алгебраические преобразования достаточно очевидны. Полученные здесь как следствие функциональные выражения носят разрывный характер в точке t = 0 . Каждое из них можно определить непосредственно только после исследования цепи для момента времени t=0+,т.е. в первый момент после коммутации.

Задача решена.

Рассмотренные здесь примеры показывают, что для цепей первого порядка нет необходимости составлять уравнения равновесия цепи, сводить эту систему к одному дифференциальному уравнению и решать соответствующее ему характеристическое уравнение. Достаточно найти входное резистивное сопротивление со стороны реактивного элемента и воспользоваться формулой (3.11) для цепи, содержащей L, или формулой (3.14) для цепи, содержащей С.

Общий вид решения для переменных состояния также известен:

Определение и производится путем исследования стационарного состояния цепи для значений .

Численные значения i_L(0-) и u_C(0-) находятся для момента времени t=0-, который предшествует коммутации. Для каждого временного состояния цепи целесообразно составить расчетную схему замещения и, пользуясь любыми методами анализа цепи, определить требуемую переменную.

Пример 3.3. Для цепи, представленной на рис.3.12, найти закон изменения напряжения на емкости С после отключения от цепи идеального источника синусоидального напряжения

До размыкания ключа S в каждом элементе цепи протекал синусоидальный ток, обусловленный источником питающего напряжения. Емкость присоединена непосредственно к источнику напряжения, и напряжение на ней в каждый момент времени такое же, как и в источнике. К моменту коммутации это напряжение будет равно

и останется на емкости в первый момент после коммутации.

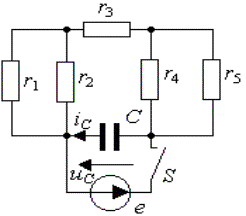
Рис. 3.12. Схема RC–цепи при питании от источника синусоидального напряжения

Переходный процесс в цепи будет развиваться за счет энергии, накопленной емкостью. В течение переходного процесса энергия электрического поля перейдет в тепловую энергию в резистивных элементах цепи. Следовательно, к концу переходного процесса напряжение на емкости станет равным нулю, что и определяет нулевое значение принужденной составляющей режима.

Проведенный предварительный анализ показывает, что переходный процесс в цепи будет определяться только свободной составляющей режима:

Постоянную времени определим по формуле (3.14), где найдем как

входное сопротивление цепи со стороны емкости:

Задача решена.

к содержанию