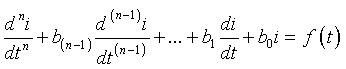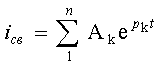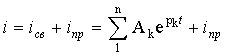3.1 Основные определения и физические условия

В учебном пособии [1], а также в первой и второй части настоящего пособия исследовались стационарные (установившиеся) режимы работы электрической цепи, когда такие интегральные характеристики как показания электроизмерительных приборов - амперметров, вольтметров, ваттметров оставались неизменными в течение достаточно долгого интервала времени, когда наблюдаемая на экране осциллографа форма тока или напряжения также оставалась неизменной на каждом интервале периода T. Это имело место в цепях, где действовали источники сигналов постоянного, синусоидального и негармонического периодического тока. В более общем случае задача анализа цепи сводится к изучению переходных процессов (характеристик) цепи, возникающих при переходе от одного стационарного режима к другому. Переходные процессы могут быть вызваны включением, отключением или переключением каких либо элементов в цепи, где действуют источники энергии. Такое изменение структуры цепи называется коммутацией.

Коммутацию в цепи показывают в виде ключа, сопротивление которого равно нулю, если ключ замкнут, и бесконечно велико, если ключ разомкнут. На схемах обычно изображают положение ключа в докоммутационный период; считается, что в момент времени t = 0 ключ переходит (мгновенно) в другое положение, после чего в цепи наступает переходный процесс. Токи и напряжения в отдельных элементах цепи приходят к новым установившимся состояниям. Этот процесс не происходит мгновенно, так как при наличии в цепи реактивных элементов - индуктивностей и емкостей - энергия магнитного и электрического поля, запасенная в этих элементах, не может изменяться скачком, а имеет тенденцию монотонного непрерывного изменения с некоторой скоростью. Этот вывод математически записывается в виде двух законов коммутации:

1. Потокосцепление в индуктивности не может изменяться скачком:

(3.1)

Если в процессе коммутации индуктивность не меняет своей величины , то как следствие имеем равенство тока в индуктивности в первый момент до и после коммутации. Это же условие непрерывности функции тока будет иметь место в любой момент времени t:

(3.2)

2. Заряд на емкости не может изменяться скачком

(3.3)

Если в процессе коммутации емкость не меняет своей величины (), то, как следствие, имеем равенство напряжений на емкости до и после коммутации. Это же условие непрерывности функции напряжения будет иметь место в любой момент времени t

(3.4)

Функции тока и напряжения , изменяющиеся монотонно, без скачков, играют ключевую роль при анализе переходных процессов; они носят название переменных состояния. Все остальные переменные (например, токи и напряжения в резистивных элементах) однозначно определяются этими функциями.

В общем случае анализ переходных процессов в линейных цепях начинают с составления полной системы уравнений равновесия цепи по законам Кирхгофа [1]. Как известно, эти равенства тождественные и определяют поведение токов и напряжений в любой момент времени t. Подстановка в них компонентных соотношений типа

, ,

(3.5)

сводит эту систему к набору дифференциальных и алгебраических уравнений. Для определения искомой функции, которую можно считать реакцией цепи на коммутацию, систему уравнений сводят к одному уравнению n–го порядка с постоянными коэффициентами. Целесообразно это уравнение получить для любой переменной состояния или

(3.6)

где i = i(t) - выходная реакция (здесь ток i); f(t) - правая часть, которая определяется только известными независимыми источниками питания цепи; n - порядок электрической цепи, определяемый суммой реактивных (индуктивных n_L и емкостных n_C) элементов цепи. При этом предполагается, что схема исследуемой цепи преобразована к соединению только канонических ветвей [1].

Общее решение линейного дифференциального уравнения (3.6) ищут в виде суммы двух составляющих

(3.7)

Здесь
-называется свободной составляющей решения; она не зависит от внешних источников энергии, а обусловлена только энергией, запасенной в реактивных элементах цепи. Эта часть решения записывается как сумма n слагаемых определенного типа:

(3.8)

где A_k - постоянные коэффициенты интегрирования; - корни характеристического уравнения.

Характеристическое уравнение получается из исследуемого дифференциального уравнения посредством замены правой части на ноль (f(t) = 0) и замены операторов дифференцирования на (или )

(3.9)

Решение алгебраического уравнения (3.9) позволяет найти n корней и записать свободную составляющую решения в виде (3.8). Для всех цепей, исследуемых в курсе электротехники, корни характеристического уравнения либо отрицательны, либо комплексно-сопряженные с отрицательной вещественной частью. Это в свою очередь означает, что свободная составляющая решения с изменением времени от t=0 до постепенно уменьшается и становится равной нулю, и тогда реакция цепи будет определяться только вторым слагаемым выражения (3.7).

Второе слагаемое называется принужденной составляющей решения; она зависит от правой части уравнения (3.6), т.е. от вида приложенного к цепи сигнала, вырабатываемого источниками питания, и параметров цепи. Наиболее просто принужденная составляющая может быть определена, если действие внешних источников воздействия на цепь носит стационарный характер, например, постоянный или гармонический. В этом случае анализируют токи и напряжения в цепи в момент времени , т.е. когда переходный процесс в цепи закончен и цепь находится в новом установившемся состоянии.

Итак, общее решение уравнения (3.6) имеет вид

Из математической теории решения линейных дифференциальных уравнений следует (задача Коши), что для определения постоянных интегрирования - необходимо знать n начальных условий в виде значений искомой функции, и ее (n - 1) производных при

t=0:

Эти значения должны быть найдены из анализа исходной цепи как в докоммутационный момент времени

t = 0-, так и в первый момент после коммутации t = 0+.

Приведенную здесь общую схему анализа переходных процессов на основе решения дифференциального уравнения называют классическим методом.

к содержанию