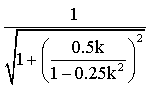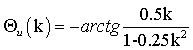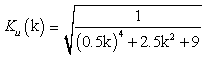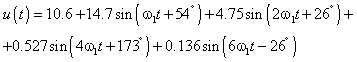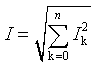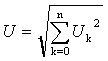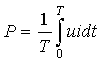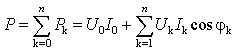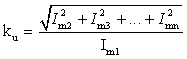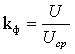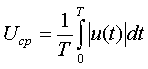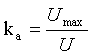2.2 Определение реакции линейной цепи на действие

негармонического периодического сигнала

Как было показано в первом разделе настоящего пособия, передаточные функции двухполюсников и четырехполюсников - АЧХ и ФЧХ на разных частотах имеют неодинаковые значения. Следовательно, электрическая цепь реагирует на каждую гармонику входного сигнала по разному, что приводит к изменению спектрального состава выходного сигнала и как следствие изменению его формы. Задача определения формы выходного сигнала сводится к использованию выражения (1.20), посредством которого можно найти спектральный состав выходного сигнала:

(2.3)

т.е. комплексная амплитуда реакции (тока или напряжения) равна произведению комплексной передаточной функции цепи - двухполюсника или четырехполюсника на комплексную амплитуду входного воздействия (источника тока или напряжения). Так как входное воздействие определяется целочисленным спектром гармоник, условие (2.3) надо рассматривать для каждой k - той гармоники отдельно, полагая вместо непрерывной переменной ω набор дискретных частот ω_k=kω₁, где ω₁ - частота первой (основной)

гармоники входного сигнала:

или, сравнивая отдельно модули и аргументы правой и левой части, найдем

(2.4)

Полученные выражения можно пояснить с помощью блок-схем:

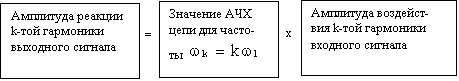
Совокупность парных значений амплитуд и начальных фаз гармоник выходного сигнала полностью определяет закон изменения и форму реакции цепи. Используя принцип наложения, найдем выходной сигнал как сумму гармоник:

или

(2.5)

где под f₂ следует понимать закон изменения тока или напряжения выходного сигнала. Многократность расчета спектра гармоник по одним и тем же формулам, где изменяется только одна переменная, делает целесообразным сведение результатов расчета в таблицу, привязав все расчеты к одной дискретной переменной. Если вычисления производятся с помощью ЭВМ, то в программе вычисления следует организовать цикл, в котором изменяется целочисленная переменная k, а внутри цикла происходит вычисление спектрального состава гармоник по формулам (2.4). Результаты расчета можно организовать в виде массива данных, а затем вывести их на печать в форме таблицы.

Если характеристики электрической цепи (АЧХ и ФЧХ двухполюсников и четырехполюсников) записывались и строились в зависимости от относительной переменной Ω=wL/r — для RL цепей и, соответственно, - для RC цепей, то при замене непрерывной переменной на дискретную переменную получим, где — реактивное индуктивное сопротивление первой (основной) гармонике сигнала, или

= rCk = r/xk, где x= 1/C — реактивное емкостное сопротивление первой гармонике сигнала. Обычно эти сопротивления задаются условиями задачи, и отношения x/r и r/x_C1 принимают вид констант, что упрощает вид конечных выражений и в дальнейшем облегчает расчет.

Точно также для цепей, содержащих полный набор элементов r, L, C, переход в выражениях для АЧХ и ФЧХ коэффициентов передач от непрерывной переменной к дискретной позволяет выделить в явном виде сопротивления реактивных элементов первой гармонике сигнала: x= L; x= 1/(C). Если эти величины заданы в исходных данных к задаче, то частотные характеристики, как и входной сигнал, также будут определяться целочисленной переменной k. Например, в примере 1.11, где коэффициент передачи напряжения определяется выражениями (1.34) и (1.35) эта замена при условии дает:

^(k)= =

При расчетах число слагаемых ряда Фурье n ограничивают, исходя из требований задачи. Допустимо удерживать в сумме лишь те слагаемые, амплитуды которых не могут рассматриваться как пренебрежимо малые. Для определения некоторых интегральных инженерных характеристик, например, действующих значений токов и напряжений, показаний приборов, коэффициентов формы, амплитуды, нелинейных искажений и т.п. достаточно удерживать в расчетах n = 3 - 5 членов ряда.

Пример 2.3. В цепочечной схеме RC фильтра нижних частот (рис. 1.17а,б) определить напряжение сигнала на выходе (t), если на входе действует негармонический сигнал однополупериодного выпрямления (табл.2 - 8) с известной величиной V = 100 B.

Для решения задачи необходимо задать либо численные значения параметров r, C, а также период T (или ω), либо их комбинацию, позволяющую сделать переход от относительной переменной Ω к дискретной переменной k. Как указывалось выше (см. пример 1.12), АЧХ и ФЧХ всех коэффициентов передачи в этом примере определялись через относительную переменную Ω = rC. Замена ω на k дает , где — реактивное емкостное сопротивление первой гармонике сигнала. Для численного решения задачи достаточно задать отношение r/. Пусть оно, например, равно 0,5; тогда в формулах для коэффициента передачи напряжения (1.36) и (1.37) следует сделать подстановку Ω = 0,5 k. В результате получим:

Подставляя целочисленные значения k определяем требуемые для анализа ординаты АЧХ и ФЧХ цепочечной RC схемы фильтра нижних частот. Все расчетные значения сведены в таблицу 3 (см. третий и четвертый столбец). В эту же таблицу записаны значения амплитуд и начальных фаз гармоник входного воздействия (2.2) - пятый и шестой столбец. Амплитуды гармоник выходного сигнала получаем путем перемножения численных значений третьего и пятого столбца, а результат записываем в седьмой столбец. Начальные фазы выходного сигнала получаем сложением четвертого и шестого столбца, а результат записываем в восьмой столбец. По данным седьмого и восьмого столбца формируем искомый гармонический ряд:

(2.6)

В полученном выражении отношение амплитуд первой и нулевой гармоники равно 1,39, т.е. примерно такое же как и во входном сигнале - 1,57; это означает, что низшие частоты проявляют себя в выходном и входном сигнале одинаково в равной мере затухая на выходе. Что касается высших гармоник, то они значительно затухают и мало влияют на форму выходного сигнала.

Таблица 3.

	K	Ku(k)	, град.	U1k, B		U2k, B
0	0	0,333	0	31,8	-	10,6	-
0,5	1	0,294	-36	50,0	90	14,7	54
1,0	2	0,224	-64	21,2	90	4,75	26
1,5	3	0,165	-83	0	-	0	-
2,0	4	0,124	-97	4,25	-90	0,527	173
2,5	5	0,095	-108	0	-	0	-
3,5	6	0,075	-116	1,82	90	0,136	-26

Для того чтобы посмотреть форму выходного сигнала, необходимо просуммировать гармоники выражения (2.6), но для этого необходимо оценить шаг приращения аргумента . Его следует задать таким, чтобы не "пропустить" высшую гармонику ряда (для нашего примера это шестая гармоника). Можно, например, принять такое условие, чтобы на периоде изменения шестой гармоники было хотя бы шесть точек суммирования:. Период шестой гармоники в шесть раз меньше периода первой гармоники, т.е.. Когда первая гармоника завершит один цикл изменения, шестая гармоника уложится в этом периоде T₁ шесть раз; следовательно, при выбранном временном шаге получим для первой гармоники и всего сигнала шаг. После перехода к радианной (градусной) мере изменения аргумента, путем умножения левой и правой части на, найдем:радиан или градусов.

Если задать условие, то получим шаг суммирования радиан или градусов. При увеличении числа гармоник ряда шаг суммирования выбирается по высшей гармонике, а число точек для высшей гармоники должно быть не менее четырех. Процесс суммирования ряда и распечатка графика легко выполняется на ЭВМ: следует организовать цикл вычислений по переменной x c шагом , и результаты суммирования гармоник на каждом шаге записать в массив, а затем распечатать содержание массива в виде графика или таблицы пошаговых значений.

На рис. 2.4 приведен график изменения выходного сигнала u (t), полученный на основании решения (2.6) и с учетом указанных выше условий.

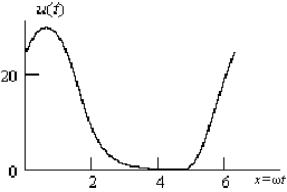
Рис. 2.4. График результирующего выходного сигнала напряжения

Задача решена.

Кроме исследования формы выходного сигнала анализируют интегральные характеристики, которые используются в инженерной практике. Они указывают на отличие несинусоидальной периодической кривой от первой гармоники этого сигнала. Этими характеристиками являются:

а. Действующее значение напряжения или тока. Показания приборов. В теории цепей доказывается, что, используя известное определение действующего значения периодической функции, формулы для вычисления действующих значений негармонических токов и напряжений принимают вид:

,

(2.7)

где и - действующие значения k-х гармоник, связанные с амплитудными значениями известными условиями:

После подстановки в выражения (2.7) получим:

Электроизмерительные приборы - амперметры и вольтметры - электродинамической, электромагнитной и тепловой систем реагируют, градуируются и измеряют, соответственно, действующее значение тока или напряжения.

б. Активная мощность.

По определению это среднее значение мгновенной мощности за период

Если подставить в это выражение ток и напряжение в виде ряда Фурье, то получим активную мощность негармонического сигнала как сумму активных мощностей k-х гармоник:

(2.8)

в. Коэффициент искажений.

Коэффициентом искажений называется отношение геометрической суммы амплитуд высших гармонических составляющих к амплитуде первой гармоники сигнала. Этот коэффициент выражается в относительных числах или процентах.

(2.9)

Очевидно, что вместо амплитуд могут сравниваться действующие значения гармоник. Коэффициент характеризует долю высших гармоник в негармонической кривой тока или напряжения. Он указывает на качественные характеристики передачи электрических сигналов электронных и радиотехнических устройств.

г. Коэффициент формы.

Коэффициентом формы называют отношение действующего значения негармонического сигнала к среднему по модулю значению.

(2.10)

где U определяется формулой (2.7), а выражением

Например, для гармонического сигнала - синусоиды это отношение равно 1.11. Отличие от этого значения указывает на долю высших гармоник в кривой негармонического сигнала.

Коэффициент используется в энергетике и преобразовательной технике.

д. Коэффициент амплитуды.

Коэффициентом амплитуды называют отношение максимального значения функции негармонического сигнала к действующему значению

(2.11)

где действующее значение определяется формулой (2.7), а максимальное значение функции - выброс сигнала может быть найден по осциллограмме или после построения выходного сигнала в виде графика. Эта задача обсуждалась в примере 2.1.

Коэффициент используется в энергетике и преобразовательной технике.

Изучение материала второй части пособия рекомендуется завершить

решением задач Приложения. Варианты заданий выбираются самостоятельно или указываются преподавателем.

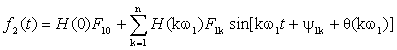
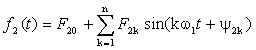
к содержанию