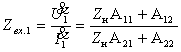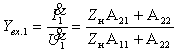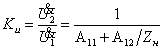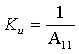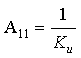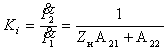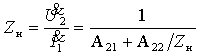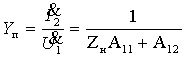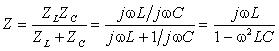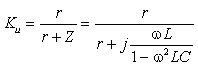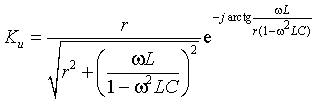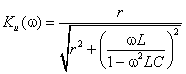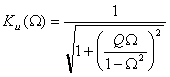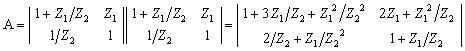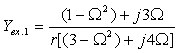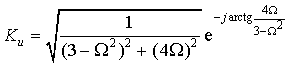1.5 Определение внешних частотных характеристик

четырехполюсников через A параметры

Частотные характеристики четырехполюсника определены выражениями (1.11) - (1.17) в самой общей форме. Однако если взять за основу уравнения четырехполюсника (1.20) и добавить к ним соотношение, связывающее ток и напряжение в нагрузке: , то эти характеристики записываются через А - параметры:

1. Входное сопротивление со стороны первичных зажимов:

(1.25)

2. Входная проводимость со стороны первичных зажимов:

(1.26)

3. Коэффициент передачи по напряжению:

(1.27)

В частном случае, когда Z_н =, т.е. имеет место режим холостого хода, получим

4. Коэффициент передачи по току:

(1.28)

В частном случае, когда Z_н = 0, т.е. имеет место режим короткого замыкания в нагрузке, получим

5. Передаточное сопротивление:

(1.29)

6. Передаточная проводимость:

(1.30)

Пример 1.11. Найти коэффициент передачи по напряжению для цепи, представленной на рис. 1.16а.

Четырехполюсник представляет собой "продольное" звено (рис. 1.16(б)) с эквивалентным сопротивлением:

Используя результат ранее рассмотренного примера 1.7, получим набор А- параметров

A11=1 A12=Z

A21=0 A22=1

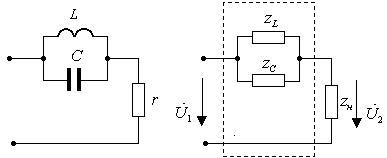
а) б)

Рис.1.16. Схема продольного реактивного звена, нагруженного на резистивное сопротивление: а)исходная цепь; б)комплексная схема

Тогда по формуле (1.27) с учетом равенства Z_н=r найдем коэффициент передачи по напряжению

Запишем полученное выражение в показательной форме, выделяя АЧХ и ФЧХ искомой частотной характеристики

где АЧХ	(1.31)
ФЧХ	(1.32)

В цепях при наличии полного набора элементов r, L, C целесообразно также ввести в рассмотрение относительную частоту, определив ее в долях резонансной частоты колебательного контура. Для данного примера имеем:

- резонансная частота колебательного контура;

- относительная частота (обобщенная переменная);

- волновое сопротивление;

- добротность колебательного контура.

С учетом введенных обозначений выражения (1.31) и (1.32) принимают вид:

Задача решена.

Пример1.12. Найти А - параметры цепочечной схемы RC фильтра нижних частот (рис. 1.17а). По найденным параметрам определить коэффициенты передачи , , , , , .

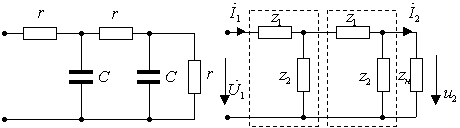
а) б)

Рис. 1.17. Схема RC фильтра нижних частот:а)исходная цепь;

б)комплексная схема

Решение задачи начинаем с изображения комплексной расчетной схемы замещения расчетной цепи (рис. 1.17б), где ; . Исследуемую цепь можно представить в виде каскадного соединения двух одинаковых четырехполюсников, рассмотренных в примере 1.10.

На основании (1.24) найдем А - параметры исследуемой схемы, перемножив две одинаковые матрицы.

Для определения коэффициентов передачи воспользуемся полученными ранее выражениями (1.25) - (1.30), и после подстановки в них комплексных параметров ; _; Z_н=r, а также с учетом относительной переменной Ω=ωCr, найдем:

1. Входное сопротивление четырехполюсника:

2. Входную проводимость:

3. Коэффициент передачи по напряжению:

4. Коэффициент передачи по току:

5. Передаточное сопротивление:

6. Передаточную проводимость:

Каждое из полученных выражений следует записать в показательной форме, чтобы выделить АЧХ и ФЧХ. Например, для коэффициента будем иметь

или

АЧХ	(1.33)
ФЧХ	(1.34)

На рис. 1.18а,б показано поведение АЧХ и ФЧХ функции .

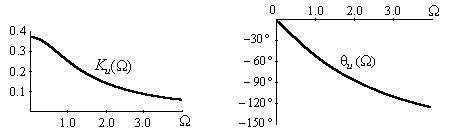
а) б)

Рис. 1.18. Частотные зависимости коэффициента передачи напряжения К_u

RC фильтра: а)АЧХ; б)ФЧХ

Анализ показывает, что RC фильтр нижних частот обеспечивает плавное уменьшение амплитуд гармонических сигналов с ростом частоты. При этом даже для очень низких частот, близких к нулю, имеет место трехкратное уменьшение сигнала на выходе. Фазовая характеристика указывает на увеличение модуля угла сдвига фаз с ростом частоты. Для частот Ω > 1.73 этот угол превосходит по величине 90˚.

Задача решена.

Изучение материала первого раздела пособия рекомендуется завершить решением задач приложения 1. Вариант указывается преподавателем или выбирается самостоятельно.

к содержанию