1.4 Частотные
характеристики четырехполюсников
Пассивный четырехполюсник представляет
собой электрическую цепь, внутри которой имеется соединение элементов r, L
и C. Цепь имеет две пары зажимов: к
первичным зажимам подсоединяется источник энергии (тока или напряжения), к
вторичным зажимам - нагрузка, под которой в общем случае понимают пассивный или
активный двухполюсник с известными вольтамперными характеристиками. На рис.1.1б
изображена комплексная схема замещения четырехполюсника; на ней указаны токи и
напряжения входных и выходных зажимов в виде комплексных переменных. Также как
и в двухполюснике, связь между этими переменными может быть определена через
частотные характеристики четырехполюсника:
1. Входное сопротивление четырехполюсника
|
|
(1.11) |
2. Входная проводимость четырехполюсника
|
|
(1.12) |
3. Коэффициент передачи по напряжению
|
|
(1.13) |
4. Коэффициент передачи по току
|
|
(1.14) |
5. Передаточное сопротивление
|
|
(1.15) |
6. Передаточная проводимость
|
|
(1.16) |
Все эти формулы определяют
причинно-следственную связь между заданным входным воздействием и реакцией цепи
в виде тока или напряжения на входных или выходных зажимах. Также как и в
двухполюсниках, все частотные характеристики не зависят от величин токов и
напряжений, а определяются только параметрами элементов цепи и способом
соединения ветвей. Они могут быть найдены опытным или расчетным путем. Все
указанные выше характеристики называют внешними
характеристиками четырехполюсника.
Некоторые из характеристик представляют
собой частотную зависимость безразмерной величины, если сопоставляются
колебания одной физической природы (напряжения с напряжением или тока с током),
либо величины, имеющие размерность сопротивления [Ом] или проводимости [См].
Фазо-частотная характеристика - ФЧХ представляет собой зависимость разности фаз
двух гармонических колебаний безотносительно к их физической природе. Эта
разность может измеряться в градусах или в радианах.
Чтобы рассчитать комплексную передаточную
функцию четырехполюсника в общем случае необходимо проделать следующее:
1. Задаться произвольным значением ![]() или
или ![]() на входе (обобщенная
функция
на входе (обобщенная
функция ![]() ).
).
2. Любым методом рассчитать комплексное
напряжение ![]() или ток
или ток ![]() на выходе цепи
(обобщенная функция
на выходе цепи
(обобщенная функция ![]() ).
).
3. Взять отношение выходного значения к
входному. Входное значение при этом сокращается, получившееся выражение будет
комплексной передаточной функцией, которую в общем случае обозначают буквой H(jω).
4. Получившееся комплексное выражение
записать в показательной форме, для чего следует использовать формулы перехода
от алгебраической формы записи комплексного выражения к показательной и
обратно:
|
|
(1.17) |
5. Сравнивая отдельно модули и фазы,
выделить АЧХ и ФЧХ передаточной функции:
![]() - АЧХ передаточной
функции; (1.18)
- АЧХ передаточной
функции; (1.18)
![]() - ФЧХ передаточной
функции. (1.19)
- ФЧХ передаточной
функции. (1.19)
6. Изменяя значение переменной от 0 до
бесконечности рассчитать и построить графики функций H(ω) и θ(ω). Целесообразно данные расчетов свести в
таблицу, которую в дальнейшем можно использовать для анализа прохождения
электрических сигналов через четырехполюсник.
Пример
1.5. Найти коэффициент передачи по току для цепи, представленной на
рис.1.2. Рассчитать и построить АЧХ и ФЧХ коэффициента передачи.
В рассматриваемой задаче в качестве
выходного тока следует найти ток в индуктивности L (ток ![]() ) по входному току источника
) по входному току источника ![]() . Используя правило деления тока на части в двух
параллельно соединенных ветвях, найдем комплекс тока
. Используя правило деления тока на части в двух
параллельно соединенных ветвях, найдем комплекс тока ![]() :
:
|
|
Поделив полученное выражение на ![]() , найдем коэффициент передачи по току
, найдем коэффициент передачи по току
|
|
Выделим из полученного выражения модуль и
аргумент, записав его в показательной форме:
|
|
Окончательно запишем выражения для АЧХ и
ФЧХ как функции обобщенной переменной Ω=ωL/r
|
|
|
|
Графики найденных функций можно строить в
зависимости от переменной ω,
если известны численные значения параметров цепи r и L, или строить их в
зависимости от обобщенной переменной Ω.
На рис.1.11a,б построены эти графики,
физический смысл которых очевиден: при малых значениях ω выполняется условие ωL
<< r, и ток источника тока будет
преимущественно протекать в индуктивности, т.е. ![]() будет стремиться к
единице. На большой частоте, при выполнении условия ωL
>> r, ток источника будет в
основном протекать в сопротивлении r, а доля тока в индуктивности будет
уменьшена, т.е.
будет стремиться к
единице. На большой частоте, при выполнении условия ωL
>> r, ток источника будет в
основном протекать в сопротивлении r, а доля тока в индуктивности будет
уменьшена, т.е. ![]() будет стремиться к
нулю.
будет стремиться к
нулю.
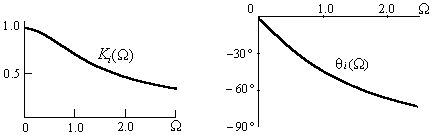
а) б)
Рис.1.11.
Частотные характеристики четырехполюсника для коэффициента передачи тока Кi:
а)АЧХ для Кi;
б) ФЧХ для Кi
Задача решена.
Пример
1.6. Для цепи, представленной на рис.1.12а найти коэффициент передачи по
току ![]() . Рассчитать и построить графики функций АЧХ и ФЧХ в
зависимости от относительной частоты
. Рассчитать и построить графики функций АЧХ и ФЧХ в
зависимости от относительной частоты ![]() [рад].
[рад].
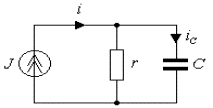
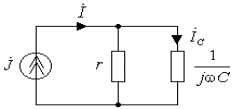
а) б)
Рис.1.12. Схема RC
цепи: а)исходная схема; б)комплексная схема
На рис.1.12б представлена комплексная
схема замещения исследуемой цепи. Используя правило деления тока на части,
найдем ток в емкостном
сопротивлении Zc = 1/jwC
![]() ,
,
откуда
|
|
|
Сравнивая модули и аргументы, получим
|
|
|
Графики функций ![]() и
и ![]() имеют такой же вид
что и графики, изображенные на рис.1.3 при условии, что r = 1 Ом. Переход к реальной переменной ω осуществляется по
формуле Ω = rCω, где произведение rC измеряется в секундах [с], если r в омах [Ом], а С в фарадах [Ф].
имеют такой же вид
что и графики, изображенные на рис.1.3 при условии, что r = 1 Ом. Переход к реальной переменной ω осуществляется по
формуле Ω = rCω, где произведение rC измеряется в секундах [с], если r в омах [Ом], а С в фарадах [Ф].
По сравнению с предыдущей задачей здесь с
ростом частоты имеет место увеличение тока в емкости, что обеспечивает
стремление к единице коэффициента передачи ![]() .
.
Задача решена.
В
общем случае, когда схема соединений элементов в цепи достаточно сложная,
четырехполюсник описывают четырьмя комплексными пара-метрами, которые связывают
между собой входные переменные ![]() ,
, ![]() с выходными
с выходными
![]() ,
, ![]() . Самой распространенной формой записи этой
связи являются А - параметры. Эту связь записывают в виде линейного
преобразования переменных в алгебраической или в матричной форме
. Самой распространенной формой записи этой
связи являются А - параметры. Эту связь записывают в виде линейного
преобразования переменных в алгебраической или в матричной форме
|
|
|
(1.20) |
где комплексные
коэффициенты ![]() ,
, ![]() ,
, ![]() и
и ![]() зависят как от
величин всех r, L, С элементов цепи, так
и от способа соединения ветвей (топологии цепи). Все эти комплексные параметры
независимо от сложности схемы цепи могут быть найдены опытным путем:
зависят как от
величин всех r, L, С элементов цепи, так
и от способа соединения ветвей (топологии цепи). Все эти комплексные параметры
независимо от сложности схемы цепи могут быть найдены опытным путем:
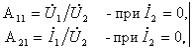 ,
,
что означает режим холостого хода на выходе (![]() ), а также
), а также
|
A12
= U1 /I2 |
при U2 = 0 |
|
A22
= I1 /I2 |
при U2 = 0 |
что означает режим короткого замыкания на выходе
(![]() ).
).
Для постановки опыта достаточно иметь два
вольтметра, два амперметра и прибор, например, двухлучевой осциллограф, с помощью
которого можно измерить угол сдвига фаз между двумя сигналами синусоидальной
формы.
Если схема четырехполюсника известна, то
эти коэффициенты могут быть найдены расчетным путем, используя законы Ома и
Кирхгофа, метод контурных токов или узловых потенциалов, а также простейшие
преобразования цепи. Все эти методы предполагают постановку и решение прямой
задачи электротехники, т.е. произвольное задание источника энергии на входных
зажимах и последующий поиск тока или напряжения в ветви, присоединенной к
выходным зажимам [1].Однако существует метод непосредственного определения
частотных характеристик четырехполюсника по известным А параметрам
четырехполюсника, о чем будет сказано ниже. Рассмотрим примеры определения А
параметров простейших четырехполюсников.
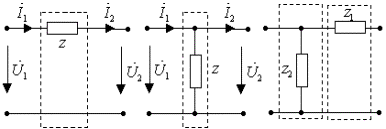
Пример 1.7.
Определить А параметры "продольного" звена, обра-зованного
эквивалентным комплексным сопротивлением Z
(рис.1.13а).
а)
б) в)
Рис.1.13. Схема простейших
четырехполюсников: а)продольное звено; б)поперечное звено; в)Г-образное звено
Решение получим на основании законов
Кирхгофа:
|
|
|
где матрица А
параметров имеет вид
|
|
(1.21) |
Задача
решена.
Пример
1.8 Определить А параметры "поперечного" звена, образованного
одним комплексным сопротивлением Z
(рис.1.13б).
Решение получим на основании законов
Кирхгофа:
|
|
|
где
матрица А параметров имеет вид
|
|
(1.22) |
Задача решена.
Для более сложных цепей есть возможность
разбиения исходной цепи на группу каскадно соединенных звеньев. Каскадным
называется такое соединение двух и более четырехполюсников, когда выходные
зажимы предыдущего четырехполюсника соединяются с входными зажимами
последующего (см. рис.1.14).
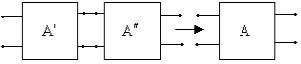
Рис.1.14.
Каскадное соединение четырехполюсников: а)соединение двух четырехполюсников;
б)результирующий четырехполюсник
Известно правило объединения матриц
каскадно соединенных четырехполюсников: при каскадном соединении перемножаются
матрицы А параметров, и задача исследователя заключается в разбиении исходной
цепи на группу простейших каскадно соединенных четырехполюсников с известными А
параметрами.
Метод основан на известном правиле
линейной алгебры умножения строк первой матрицы на столбцы второй:
|
|
Если число каскадно соединенных звеньев
больше двух, то следует перемножать матрицы в той последовательности, в которой
стоят четырехполюсники, помня о том, что перемножение матриц обладает
сочетательным свойством, но не коммутативно, т.е.![]() .
.
Пример
1.9. Найти А параметры Г - образного звена, образованного каскадным
соединением "поперечного" и "продольного" звена
(рис.1.13в).
При решении этой задачи уже может быть
использован метод перемножения А матриц, где на первом месте должна стоять
матрица поперечного звена, а на втором - продольного.
|
|
(1.23) |
Задача решена.
Пример 1.10.
Найти А параметры обратного к Г - образному звену, образованному каскадным
соединением "продольного" и "поперечного" звена (рис.1.15).
По сравнению с предыдущей задачей следует
поменять местами перемножаемые матрицы:
|
|
(1.24) |
Из сравнения выражений
(1.23) и (1.24) видим, что результирующие матрицы отличаются друг от друга
только заменой элементов А11 на А22 и
наоборот.
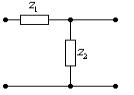
Рис.1.15. Каскадное соединение
продольного и поперечного звена
Задача решена.
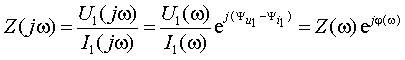
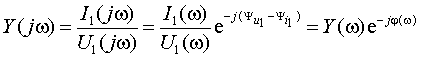
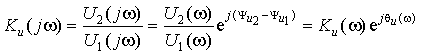
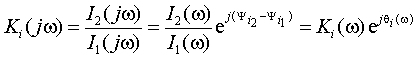
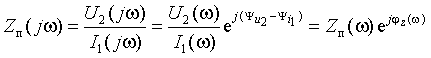
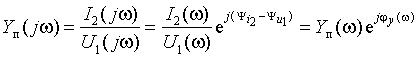
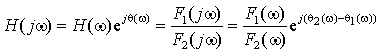
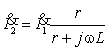
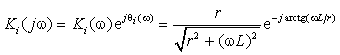
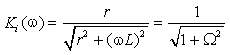
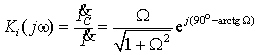
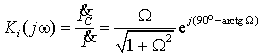
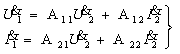 или
или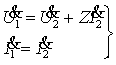
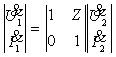
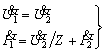
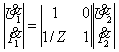 ,
,