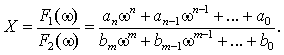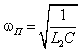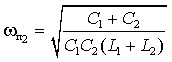1.2 Частотные характеристики реактивных двухполюсников

Реактивным называют двухполюсник, включающий только индуктивные и емкостные элементы. Такой двухполюсник называется приведенным, если число индуктивностей отличается от числа емкостей не более чем на единицу. Любой реактивный двухполюсник может быть преобразован к схеме приведенного двухполюсника. Так как реактивный двухполюсник представляет собой цепь без потерь, то его входное сопротивление будет определяться чисто мнимым выражением Z = jX , где Х имеет вид дробно-рациональной функции

(1.3)

Полином числителя F₁ имеет степень n, а полином знаменателя F₂ -

степень m; коэффициенты полиномов a и b определяются топологией цепи и конкретным набором реактивных элементов в каждой ветви исследуемой цепи. Для приведенного двухполюсника степени полиномов n и m отличаются друг от друга не более чем на единицу.

При исследовании зависимостей АЧХ и ФЧХ реактивных двухполюсников необходимо учитывать те значения w , когда числитель или знаменатель выражения (1.3) обращаются в ноль. Эти значения находятся как корни полиномов или . Физический смысл корней определяется конечным набором резонансных состояний исследуемой цепи. Различают два типа резонанса: резонанс напряжений, когда реактивная часть входного сопротивления двухполюсника обращается в нуль, и резонанс токов, когда реактивная часть входной проводимости двухполюсника обращается в ноль. Для реактивных двухполюсников входное сопротивление и входная проводимость являются величинами взаимообратными. Следовательно, нули функции (1.3), которые совпадают с корнями полинома F₁, определяют точки резонансов напряжений, а полюса функции (1.3), совпадающие с корнями полинома , определяют точки резонансов токов. Набор резонансных частот называют нулевыми и полюсными частотами, каждой из них приписывается свой цифровой индекс. В крайних точках частотного диапазона: ω = 0 и ω = ∞ функция X (или обратная к ней функция B = 1/X) принимает значение ноль или бесконечность, т.е. в этих точках можно наблюдать наличие "вырожденного" резонанса напряжений или токов. Как следует из предыдущего рассмотрения, число полюсных частот отличается от числа нулевых частот не более чем на единицу. Из теории электрических цепей также следует:

1. В приведенном двухполюснике общее число резонансных частот на единицу меньше числа реактивных элементов цепи;

2. Нули и полюса функции X (или B) обязательно чередуются, т.е. не могут рядом находиться две нулевые или две полюсные частоты;

3. С увеличением частоты функция X (или B) имеет только возрастающий характер, т.е. всегда выполняется условие dX/dω > 0 (соответственно dB/dω > 0);

4. Для всех частот, отличных от резонансных, входное сопротивление двухполюсника принимает или индуктивный (Z = +jX), или емкостной

(Z=– jX) характер. При переходе каждой резонансной точки характер входного сопротивления меняется на обратный;

5. Из предыдущего пункта следует, что фазочастотная характеристика (ФЧХ) принимает одно из двух значений φ(ω) = + 90˚ или φ(ω) = - 90˚. И только в резонансных точках φ = 0, как это следует из определения резонанса.

Пример 1.2. Для электрической цепи рис.1.4а найти в общем виде выражения для нулевых и полюсных частот функции входного сопротивления. Построить качественно график зависимости X(ω) и фазочастотную характеристику.

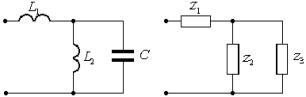
а) б)

Рис. 1.4. Схема реактивного двухполюсника: а)исходная схема; б)комплексная схема

Решение задачи начинаем с изображения комплексной схемы замещения исходной цепи (рис.1.4б), где ₁; Z₂ = jwL₂; . Эту схему в дальнейшем формально анализируем как цепь постоянного тока. Используя правило объединения параллельно и последовательно соединенных элементов, найдем входное сопротивление:

(1.4)

Приравнивая к нулю числитель полученного выражения, найдем нулевые частоты:

(1.5)

В этой точке (на постоянном токе) сопротивление действительно равняется нулю, а затем с увеличением частоты возрастает, сохраняя индуктивный характер. Расположение найденных резонансных частот показано на рис.1.5а. Здесь же построен график зависимости X(ω), который объединяет свойства АЧХ и ФЧХ функции входного сопротивления и отличается от АЧХ только знаком для отрицательных значений ординат (Z(ω) = X(ω)).

Из сравнения выражений (1.4) и (1.5) следует, что нулевая частота расположена правее полюсной частоты , т.е. за вырожденным нулем следует полюс, затем снова ноль . При очень большой частоте получаем вырожденный полюс функции: , т.е. график роста функции на больших частотах ограничен этой прямой. При увеличении w в каждой полюсной точке функция X(ω) меняет знак с плюса на минус, а в нулевой точке - с минуса на плюс; при этом соответственно изменяется и характер входного сопротивления. На рис.1.5б показана фазочастотная характеристика функции Z( jω).

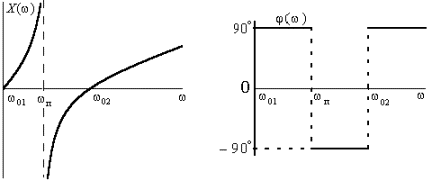
а) б)

Рис. 1.5. Частотные характеристики входного сопротивления реактивного двухполюсника: а)зависимость X(ω)=Z/j; б)ФЧХ

Задача решена.

Пример 1.3. Для электрической цепи рис.1.6а найти нулевые и полюсные частоты. Построить качественно график зависимости X(ω) от частоты.

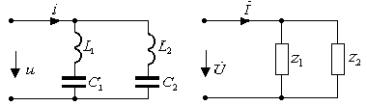
а) б)

Рис. 1.6. Схема реактивного двухполюсника: а)исходная схема; б)комплексная схема

Предварительный анализ цепи показывает, что при наличии четырех реактивных элементов в цепи будут три резонансных режима, не считая вырожденных резонансов в точках ω = 0 и ω = ∞. На рис.1.6б изображена комплексная схема замещения исходной цепи, где сопротивления ветвей

Найдем проводимость двухполюсника как сумму проводимостей параллельно соединенных ветвей

Входное сопротивление определим как величину, обратную проводимости

Приравнивая к нулю числитель F₁ этого выражения, найдем нулевые частоты, т.е. точки резонанса напряжений:

, .

Приравнивая к нулю знаменатель, найдем полюсные частоты, т.е. точки резонанса токов:

Построение графика начинается с вырожденной полюсной частоты=0. На этой частоте (постоянном токе) индуктивные элементы имеют нулевое сопротивление, а емкостные – бесконечно большое; поэтому график начинается со значения минус бесконечность. Затем функция возрастает, проходя первую нулевую частоту. Если считать, что выполняется условие L₁C₁>L₂C₂, то первой нулевой частотой будет значение .

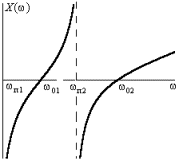
Рис. 1.7. Зависимость функции входного сопротивления X(ω)=Z/j от частоты

После перехода через ноль функция становится положительной, что характеризует индуктивный характер входного сопротивления, и возрастает до бесконечности, достигая полюсной частоты . При переходе через полюс знак функции X(ω) изменяется снова на минус, что характеризует емкостной характер входного сопротивления. Дальнейший рост функции приводит к очередной нулевой частоте (точка ) и смене знака на плюс. На больших частотах ω>> сопротивление двухполюсника принимает индуктивный характер и изменяется по линейному закону: , где эквивалентное значение индуктивности определяется формулой параллельного соединения элементов и . При стремлении ω к бесконечности придем снова к вырожденному полюсу.

Задача решена

к содержанию