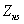 , по ней будет проходить ток:
, по ней будет проходить ток:5.1.1. Синусно - косинусный поворотный трансформатор.
При подключении к синусной обмотке S нагрузки 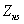 , по ней будет проходить ток:
, по ней будет проходить ток:
|
|
(5.1.9) |
где
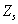 - сопротивление обмотки S, которое будем считать постоянным.
- сопротивление обмотки S, которое будем считать постоянным.
Ток IHS создает НС ротора, максимальное значение которой
|
|
(5.1.10) |
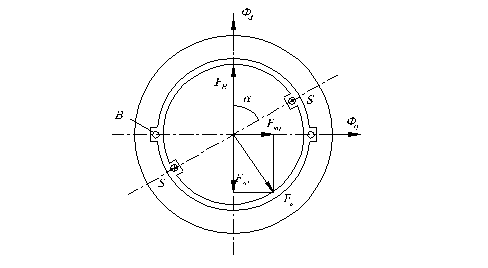
Рис. 5.3. Векторная диаграмма НС при подключении нагрузки к синусной обмотке.
Как видно из рис. 5.3 ось этой НС совпадает с осью фазы S, поэтому ее можно представить в виде векторной суммы двух составляющих: продольной Fsd=Fssinα и поперечной Fsq=Fscosα. Продольная составляющая Fsd создает в обмотке возбуждения В компенсирующий ток, НС которого FB , так же, как и в обычном трансформаторе, компенсирует действие Fsd . Результирующий продольный поток Фd индуцирует в обмотке S ЭДС
|
|
(5.1.11) |
Поперечная составляющая Fsq создает в поворотном трансформаторе поперечный поток Фq , максимальное значение которого
|
|
(5.1.12) |
где
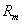 - магнитное сопротивление магнитопровода машины.
- магнитное сопротивление магнитопровода машины.
По отношению к поперечному потоку Фq обмотка S является косинусной и, следовательно, в ней индуцируется ЭДС
|
|
(5.1.13) |
ЭДС Еsq можно представить в виде:
|
|
(5.1.14) |
где
|
|
(5.1.15) |
- реактивное сопротивление обмотки ротора.
Таким образом, при нагрузке в синусной обмотке S продольным и поперечным потоками индуктируется результирующая ЭДС
|
|
(5.1.16) |
Следовательно, ЭДС, индуцированная в синусной обмотке будет иметь вид:
|
|
(5.1.17) |
Решив это уравнение относительно 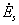 ,получим
,получим
|
|
(5.1.18) |
где
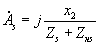 - некоторый комплексный коэффициент.
- некоторый комплексный коэффициент.
Аналогично можно получить выражение для ЭДС, индуцированной в косинусной обмотке:
|
|
(5.1.19) |
где
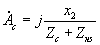 - комплексный коэффициент,
- комплексный коэффициент,
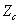 и
и 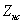 - сопротивление косинусной обмотки и подключенной к ней нагрузки.
- сопротивление косинусной обмотки и подключенной к ней нагрузки.
Таким образом, при наличии тока нагрузки 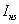 и
и 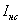 нарушаются требуемые синусоидальная и косинусоидальная зависимости изменения ЭДС Es и Ec , а, следовательно, и выходных напряжений Us и Uc от угла поворота α и возникает определенная погрешность. Относительная погрешность для синусной и косинусной обмоток:
нарушаются требуемые синусоидальная и косинусоидальная зависимости изменения ЭДС Es и Ec , а, следовательно, и выходных напряжений Us и Uc от угла поворота α и возникает определенная погрешность. Относительная погрешность для синусной и косинусной обмоток:
|
|
(5.1.20)
(5.1.21) |
где
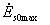 и
и 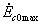 - максимальные значения напряжений
- максимальные значения напряжений 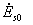 и
и 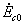 .
.
Действительная часть комплексов 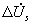 и
и 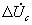 принимается за амплитудную погрешность, мнимая - за фазовую погрешность (изменение фазы выходного напряжения синусной или косинусной обмотки по отношению к фазе
принимается за амплитудную погрешность, мнимая - за фазовую погрешность (изменение фазы выходного напряжения синусной или косинусной обмотки по отношению к фазе 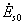 или
или 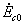 при холостом ходе). Из выражений для
при холостом ходе). Из выражений для 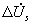 и
и 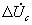 следует, что для уменьшения погрешности
следует, что для уменьшения погрешности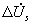 и
и 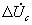 необходимо уменьшить величины комплексов
необходимо уменьшить величины комплексов 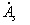 и
и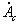 , т.е. увеличить сопротивления нагрузки
, т.е. увеличить сопротивления нагрузки 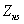 и
и 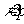 . Наименьшая амплитудная погрешность соответствует активной нагрузке; наименьшая фазовая погрешность - индуктивной и емкостной нагрузкам.
. Наименьшая амплитудная погрешность соответствует активной нагрузке; наименьшая фазовая погрешность - индуктивной и емкостной нагрузкам.
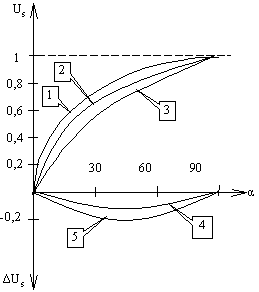
Рис. 5.4. Зависимость выходного напряжения 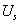 в синусной обмотке и погрешности
в синусной обмотке и погрешности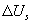 от угла поворота ротора. (1-кривая
от угла поворота ротора. (1-кривая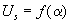 при холостом ходе;2,3- при нагрузке (
при холостом ходе;2,3- при нагрузке (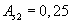 и
и 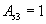 ); 4-зависимость
); 4-зависимость 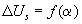 для
для 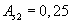 ; 5- зависимость
; 5- зависимость 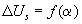 для
для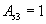 )
)
На рис. 5.4 показаны зависимости Us=f(α) οри холостом ходе (кривая 1) и при нагрузке (кривые 2 и 3), построенные по вышеуказанным формулам. При этом кривые 2 и 3 соответствуют значениям As, равным 0,25 и 1. Из этих кривых следует, что при нагрузке погрешность поворотного трансформатора может быть весьма значительной. Зависимости амплитудной погрешности ΔUs от угла поворота α для указанных значений модуля комплекса As изображены на рисунке кривыми 4 и 5.
Исследование выражений для 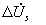 и
и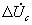 показывает, что погрешность ΔUs достигает максимального значения при углах α, равных 35о16', 144o44' и 215o16'.
показывает, что погрешность ΔUs достигает максимального значения при углах α, равных 35о16', 144o44' и 215o16'.
Для устранения погрешности поворотного трансформатора, обусловленной поперечным потоком Фq , применяют так называемое симметрирование трансформатора, т. е. компенсацию поперечного потока ротора. Существуют два способа симметрирования: вторичное (со стороны ротора) и первичное (со стороны статора).
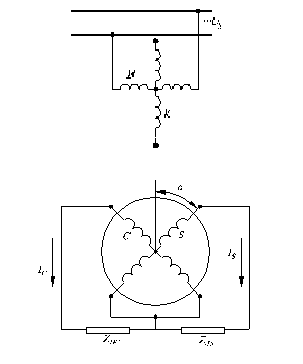
Вторичное симметрирование. Уменьшить погрешность выходного напряжения, снимаемого с синусной обмотки, можно, если подключить к косинусной обмотке сопротивление 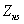 (рис. 5.5a).
(рис. 5.5a).
В этом случае ток, проходящий по обмотке С, создает намагничивающую силу, максимальное значение которой
|
|
(5.1.22) |
 а)
а)
 б)
б)
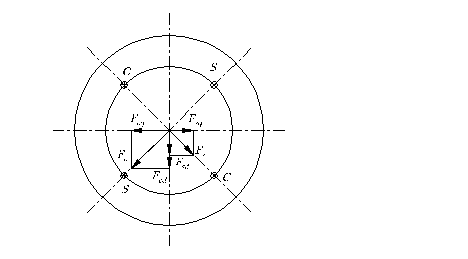
Рис. 5.5. Схема синусно-косинусного трансформатора о вторичным симметрированием (а) и диаграмма МДС, создаваемых обмотками ротора (б)
НС Fc можно представить, как и НС Fs , в виде векторной суммы двух составляющих: продольной Fcd=Fccosα θ οоперечной Fcq=Fcsinα. Οπодольная составляющая Fcd совпадает по направлению с Fsd, а поперечная составляющая Fcq направлена против Fsq. При равенстве Fcq =Fsq поперечный поток Фq будет равен нулю. Следовательно, не будет и погрешности, обусловленной этим потоком.
Величину 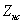 можно определить из условия
можно определить из условия
|
|
(5.1.23) |
или
|
|
(5.1.24) |
или
|
|
(5.1.25) |
Так как поперечный поток Фq равен нулю, то
|
|
(5.1.26) |
Следовательно
|
|
(5.1.27) |
Откуда
|
|
(5.1.28) |
Т.е. при равенстве результирующих сопротивлений обеих фаз ротора ток IB в обмотке возбуждения поворотного трансформатора не зависит от угла поворота ротора, т. к. в выражении для результирующей продольной составляющей НС ротора 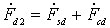 , определяющей величину тока IВ , не входит какая-либо функция угла α:
, определяющей величину тока IВ , не входит какая-либо функция угла α:
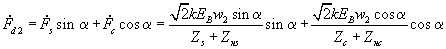
или
|
|
(5.1.29) |
где
|
|
(5.1.30) |
Недостатком этого метода симметрирования является то, что практически он применим только при неизменном сопротивлении нагрузки.
Первичное симметрирование. Если нагрузка подключена только к одной из обмоток ротора, например к обмотке S (рис. 5.6а), то НС ротора по поперечной оси не равна нулю.
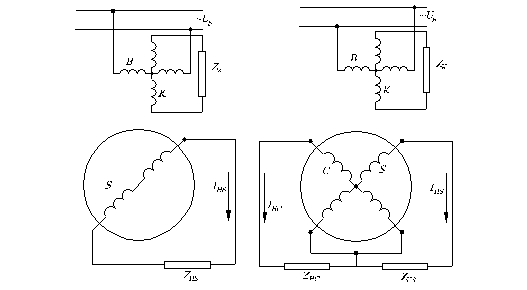
|
а) |
б) |
Рис. 5.6. Схемы синусно - косинусных поворотных трансформаторов с первичным (а) и первичным и вторичным симметрированием (б)
Для уменьшения поперечного потока компенсационную обмотку К статора замыкают на какое-либо малое сопротивление 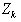 или накоротко. В этом случае по поперечной оси будет действовать результирующая НС
или накоротко. В этом случае по поперечной оси будет действовать результирующая НС
|
|
(5.1.31) |
где
|
|
(5.1.32) |
- НС, создаваемая компенсационной обмоткой.
Так как обмотка К по отношению к поперечному потоку Фq представляет собой замкнутую накоротко вторичную обмотку трансформатора, то результирующая НС 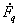 будет значительно меньше НС
будет значительно меньше НС 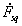 первичной обмотки. Поэтому поперечный поток Фq и вызванная им погрешность резко уменьшается. При изменении нагрузки, подключенной к обмотке ротора, НС
первичной обмотки. Поэтому поперечный поток Фq и вызванная им погрешность резко уменьшается. При изменении нагрузки, подключенной к обмотке ротора, НС 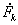 изменяется приблизительно пропорционально НС
изменяется приблизительно пропорционально НС 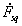 , вследствие чего степень компенсации поперечного потока остается практически неизменной. Это является достоинством данного метода симметрирования. Однако при изменении угла поворота ротора α изменяется ток
, вследствие чего степень компенсации поперечного потока остается практически неизменной. Это является достоинством данного метода симметрирования. Однако при изменении угла поворота ротора α изменяется ток 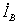 в обмотке возбуждения, что является нежелательным, т.к. при заданном напряжении
в обмотке возбуждения, что является нежелательным, т.к. при заданном напряжении 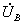 в этом случае будет изменяться ЭДС
в этом случае будет изменяться ЭДС 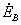 . В результате появляется дополнительная погрешность в величине выходных напряжений
. В результате появляется дополнительная погрешность в величине выходных напряжений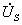 и
и 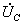 на зажимах синусной и косинусной обмоток. Поэтому в поворотных трансформаторах обычно применяют одновременно первичное и вторичное симметрирование ( рис. 5.6б).
на зажимах синусной и косинусной обмоток. Поэтому в поворотных трансформаторах обычно применяют одновременно первичное и вторичное симметрирование ( рис. 5.6б).
Рассмотренные методы компенсации поперечного потока Фq могут быть применены при использовании в качестве рабочей обмотки как синусной, так и косинусной обмоток. Поэтому поворотный трансформатор, подключенный по схеме рис. 5.6б, называют синусно - косинусным.
назад/оглавление/ вперед