1.2. Расчет магнитной цепи постоянного магнита
Постоянные магниты широко применяются в измерительных приборах, реле, генераторах и т. д.
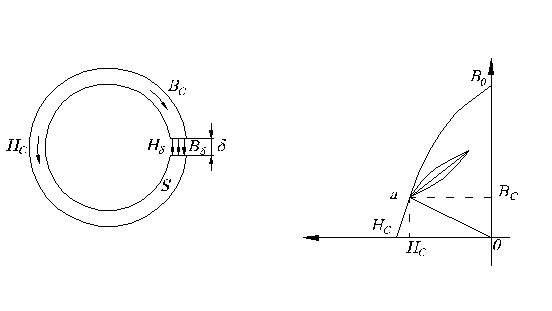
На рис.1.4 изображено тороидальное кольцо с воздушным зазором.

Рис.1.4. Тороидальный магнитопровод с воздушным зазором (а) и его кривая размагничивания (б)

Если бы не было воздушного зазора, то, как видно из кривой размагничивания (рис.1.4б), напряженность в сердечнике равнялась бы нулю Hc=0, а индукция Bc в сердечнике равнялась бы остаточной индукции B0.
Из закона полного тока имеем: 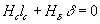 .
.
Здесь
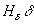 - магнитное напряжение воздушного зазора;
- магнитное напряжение воздушного зазора;
lc - длина средней линии тороида.
Напряженность магнитного поля в воздушном зазоре: 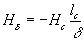 .
.
Если зазор достаточно мал, то можно пренебречь потоком рассеяния и считать, что поток в магните равен потоку в зазоре: 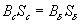 ,
,
отсюда
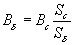 ;
; 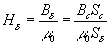 .
.
Воспользовавшись выражением 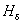 можно написать:
можно написать:
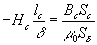 ;
;
|
|
(1.9) |
коэффициент 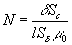 носит название размагничивающего фактора.
носит название размагничивающего фактора.
Проведем прямую Hc= -NBc из точки 0 до пересечения с кривой размагничивания (рис.1.4б). Координаты точки пересечения 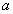 определяют напряженность магнитного поля Hc и индукцию Bc. Если теперь уменьшить величину зазора, то магнитная индукция и напряженность будут определяться не кривой размагничивания, а, в силу наличия гистерезиса, частной петлей гистерезиса. Эту петлю называют линией возврата.
определяют напряженность магнитного поля Hc и индукцию Bc. Если теперь уменьшить величину зазора, то магнитная индукция и напряженность будут определяться не кривой размагничивания, а, в силу наличия гистерезиса, частной петлей гистерезиса. Эту петлю называют линией возврата.
назад/оглавление/ вперед