Лекция №9

«Эффекты квантования и шумы в цифровых фильтрах»

            В реальных устройствах, реализующих алгоритмы цифровой обработки сигналов, необходимо учитывать эффекты, обусловленные квантованием входных сигналов и конечной разрядностью всех регистров. Источниками ошибок в процессах обработки сигналов являются округление (или усечение) результатов арифметических операций, шум квантования, связанный с аналого-цифровым преобразованием входных аналоговых сигналов, неточность реализации характеристик цифровых фильтров из-за округления их коэффициентов.

            Для анализа эффектов, связанных с конечной разрядностью представления данных, необходимо сделать некоторые предположения относительно статистической независимости различных источников шумов, возникающих в цифровом фильтре. Принимается статистическая модель, основанная на следующих предположениях:

1. Любые два отсчета шума от одного и того же источника не коррелированы.

2. Любые два источника шума создают некоррелированные шумы.

3. Шум каждого из источников не коррелирован с входным сигналом.

Эти предположения значительно упрощают анализ процессов, связанных с шумами квантования в цифровых фильтрах, поскольку делают отдельные источники шума статистически независимыми друг от друга и дают возможность проводить анализ для каждого из них отдельно. Однако, принятые предположения справедливы далеко не всегда. Можно привести множество примеров, для которых эти предположения не верны. Например, если входной сигнал является постоянным или синусоидальным, с частотой кратной частоте дискретизации. В первом случае все отсчеты ошибки квантования будут одинаковы, а во втором они образуют периодическую последовательность. Таким образом, в обоих случаях выдвинутые предположения неверны.

            Эффекты квантования приводят в конечном итоге к погрешностям в выходных сигналах цифровых фильтров, а в некоторых случаях и к неустойчивым режимам работы. В силу принятых допущений выходная ошибка цифрового фильтра вычисляется как суперпозиция ошибок, обусловленных каждым независимым источником.

            Если на вход цифрового фильтра с импульсной характеристикой h(t) поступает сигнал x(t), то выходной сигнал фильтра определяется выражением

                                            (9.1).

В результате квантования входного сигнала образуется шум квантования e_in(n), который накладывается на входной сигнал и воздействует на фильтр. В силу линейности фильтра можно вычислить реакцию фильтра e_out(n) на входной шум

                                       (9.2).

При этом подразумевается что все вычислительные устройства и запоминающие устройства фильтра имеют бесконечную разрядность.

            Аналогично можно найти ошибку сигнала в любой точке структурной схемы фильтра, обусловленную шумом квантования входного сигнала e_in(n).

                                         (9.3),

где h_i(n) – импульсная характеристика части фильтра от его входа до точки, в которой оценивается ошибка.

            Если входной сигнал фильтра квантуется с разрядностью b_in, то ошибка квантования входного сигнала при использовании округления ограничена величиной

                              (9.4),

а ошибка выходного сигнала фильтра, вызванная квантованием входного сигнала может быть оценена как

           (9.5).

Таким образом, верхняя граница ошибки, вызванной квантованием входного сигнала, зависит от разрядности квантования и от суммы модулей выборок импульсной характеристики фильтра.

            Дисперсия входного шума округления

                                                   (9.6),

поэтому дисперсия шума квантования на выходе фильтра в соответствии с (9.3) равна

                      (9.7).

Согласно равенству Парсеваля

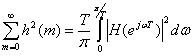                                   (9.8)

можно записать (9.7) в виде

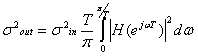                                   (9.9),

где   - амплитудно-частотная характеристика цифрового фильтра.

Таким образом, по допустимой величине s_out² и известной АЧХ или импульсной характеристике фильтра можно определить допустимую величину дисперсии ошибки входного сигнала s_in², которая в свою очередь определяет требуемую разрядность b_in квантования входного сигнала.

Отношение сигнал-шум на выходе фильтра, которое определяется как отношение мощности сигнала к мощности шума в логарифмическом масштабе определяется как

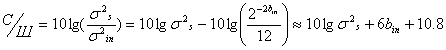         (9.10),

где s_s² – дисперсия полезного входного сигнала, а b_in – разрядность квантования входного сигнала. Следовательно, при увеличении разрядности квантования на один разряд отношение сигнал-шум увеличивается примерно на 6 дБ.

            В качестве примера рассмотрим цифровой фильтр первого порядка, описываемый уравнением

                                              (9.11).

Его структурнаясхема представлена на рис.9.1.

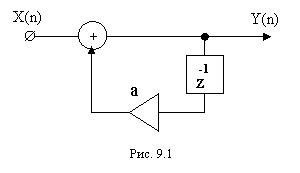
Пусть шум квантования входного сигнала имеет дисперсию s_in². Импульсная характеристика такого фильтра имеет вид

                                                                    (9.12).

Согласно (9.7) дисперсия шума выходного сигнала такого фильтра, обусловленного квантованием входного сигнала равна

                                 (9.13).

Для устойчивости фильтра необходимо выполнения условия и, следовательно, , т.е. мощность выходного шума больше мощности входного шума. Чем ближе  к единице, тем больше усиление входного шума фильтром.

            С использованием теоремы Парсеваля можно определять дисперсию выходного шума фильтра по его АЧХ. Пусть задан фильтр, АЧХ которого представлена на рис.9.2.

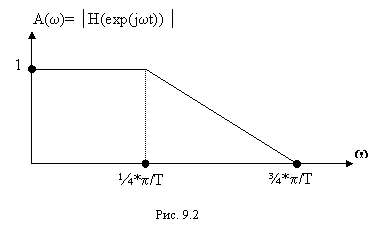Тогда, согласно (9.9) дисперсия выходного шума фильтра, вызванного квантованием входного сигнала будет равна

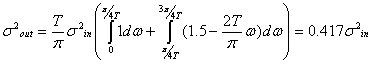               (9.14).

            Выбор оптимальной разрядности квантования входного сигнала определяется необходимой точностью представления информации, заложенной во входном сигнале, наличием в нем предвходящего шума и процедурой, которая применяется для обработки сигнала.

            Содержащийся в сигнале шум определяет верхнюю границу числа уровней квантования. Очевидно, нет смысла использовать большое количество разрядов когда в сигнале содержится большой шум, так как в этом случае с большой точностью будет квантоваться шум, а не сигнал. Достаточно выбрать столько уровней квантования, чтобы вклад шума квантования был мал по сравнению с шумом, содержащимся в сигнале.

            С другой стороны, минимально допустимое количество уровней квантования должно обеспечивать желаемое качество выходного сигнала. Ухудшение качества входного сигнала может быть вызвано воздействием неидеальностей на этапе предварительной обработки сигнала (шумы и ограниченные частотные характеристики предварительных масштабирующих усилителей и аналоговх фильтров).

            До сих пор принималось, что коэффициенты разностного уравнения фильтра заданы с бесконечной точностью. При физической реализации фильтра эти коэффициенты хранятся в элементах электронной памяти (запоминающих ячейках), которые имеют ограниченную разрядность. Это означает, что коэффициенты фильтра также как и входной сигнал подвергаются квантованию.

Квантование коэффициентов фильтра подчиняется тем же закономерностям, что и квантование входного сигнала. В результате квантования коэффициентов фильтра значения полюсов и нулей передаточной функции фильтра в большей или меньшей степени изменяются, что, в свою очередь, приводит к соответствующему изменению частотных характеристик фильтра. Так, кантование коэффициентов фильтра приводит к появлению ошибки

                                                   (9.15),

где A(w) – АЧХ фильтра с неквантованными коэффициентами, A_d(w) – АЧХ фильтра с квантованными коэффициентами. Величина  не должна превосходить допустимую величину , определяемую обычно из условия, чтобы отклонения реальной АЧХ от идеальной были в допустимых пределах.

            Различные структуры фильтров имеют различную чувствительность к изменению отдельных коэффициентов. Поэтому универсального метода определения требуемого количества разрядов квантования коэффициентов, для всех типов фильтров предложить невозможно. Необходимое количество разрядов в квантованных коэффициентах фильтров можно определить путем вычисления  для последовательно возрастающего числа разрядов в кодах коэффициентов до выполнении условия .

            Возможны и практически применяются и другие методы, в частности методы, основанные на предварительном изучении чувствительности характеристик конкретного типа фильтра к изменениям его коэффициентов.

            В качестве примера рассмотрим биквадратный блок описываемый передаточной функцией

                                          (9.16),

структурная схема которого представлена на рис.9.3.

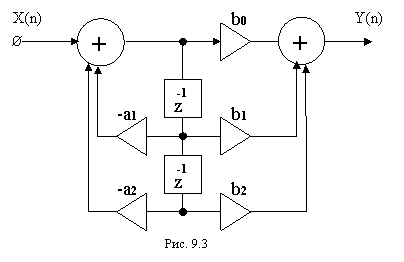
Если обозначить полюсы передаточной функции (9.16) через , то легко убедиться, что

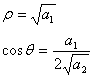                                                             (9.17).

Тогда при малых изменениях a₁ и a₂ координаты полюсов изменяются на величины

                                 (9.18),

аналогично                                                      (9.19).

Можно заметить, что Dr резко изменяется при значениях r, близких к единице, тогда как Dq резко изменяется при значениях q, близких к нулю.

            Чувствительность частотных характеристик фильтров к изменению значений коэффициентов сильно зависит от структуры, выбранной для реализации фильтра.

            При реализации алгоритма цифрового фильтра выполняются операции сложения и умножения на коэффициенты. Сложение чисел с фиксированной точкой при разрядности сумматора, не меньшей разрядностей представления слагаемых, не приводит к ошибкам округления представления суммы.

            Выполнение операции умножения связано с ошибками округления. Произведение двух чисел с фиксированной точкой с b₁ и b₂ разрядами соответственно может содержать до b₁+b₂ разрядов. При последовательном выполеннии операций умножения необходимо ограничивать разрядность произведений. Иначе, разрядность последующих произведений будет неограниченно возрастать. Поэтому, для хранения произведений обычно отводят запоминающие ячейки с разрядностью, меньшей чем до b₁+b₂. Таким образом, результат умножения подвергается округлению. В результате округления произведений алгоритм фильтра реализуется не точно и выходной сигнал вычисляется с ошибкой.

Модель умножителя с конечным числом разрядов представляется в виде последовательного соединения идеального умножителя (с неограниченным числом разрядов) и сумматора, на вход которого наряду с точным значением произведения поступает шум квантования. На выходе сумматора получается квантованное значение произведения с b_mul разрядами (рис.9.4).

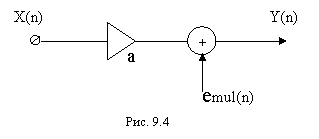
Ошибка округления одного произведения может быть оценена своей верхней границей

                       (9.20),

где Q_mul – шаг квантования произведения. Эта ошибка может рассматриваться как дискретный стационарный случайный процесс с равномерной плотностью распределения вероятности, с нулевым средним и дисперсией равной

                                                            (9.21).

Приняв такую линейную модель для каждого узла умножения на структурной схеме фильтра, можно вычислить ошибку в выходном сигнале фильтра как супкрпозицию ошибок, обусловленных всеми источниками шума округления. С этой целью следует лишь определить импульсные характеристики g_i(n) частей структуры фильтра от каждого i-го источника шума (т.е. выхода i-го умножителя) до выхода фильтра и вычислить составляющую в выходном шуме фильтра, обусловленную i-м источником шума как

                               (9.22).

Тогда, шум округления на выходе, обусловленный всеми L источниками шума можно вычислить как

                                           (9.23).

Таким образом, выходной шум фильтра, обусловленный i-м источником округления не превышает величины

     (9.24).

Тогда максимальная величина выходного шума, обусловленного всеми L источниками округления (при том, что разрядность всех умножителей одинакова) равна

                         (9.25).

На основании (9.7) можно оценить дисперсию результирующего шума округления от всех источников как

                             (9.26).

Уровень выходного шума фильтра, обусловленного квантованием произведений, сильно зависит от особенностей структуры, выбранной для реализации фильтра. Это объясняется тем, что импульсная характеристика участка фильтра от выхода конкретного умножителя до выхода фильтра зависит от применяемой структуры. При выборе структуры фильтра необходимо учитывать влияние ошибок квантования произведений наряду с ошибками квантования коэффициентов.

Все источники шума квантования произведений вносят различный вклад в результирующий выходной шум.

В качестве примера рассмотрим оценку выходного шума квантования произведений в биквадратном блоке, имеющем импульсную характеристику h(n). Шумовая модель рассматриваемой структуры  представлена на рис.9.5.

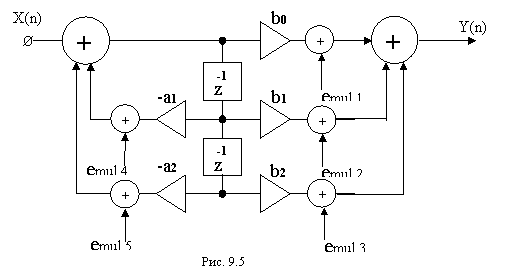
Из представленной модели видно, что структура фильтра имеет пять источников шума квантования произведений. Источники e_mul.4 и e_mul.5 проходят по той же цепи, что и входной сигнал. Это означает, что из импульсные характеристики g₄(n) и g₅(n) совпадают с общей импульсной характеристикой фильтра h(n). Источники e_mul.1, e_mul.2,  e_mul.3 непосредственно добавляют ошибку на выходе фильтра, вследствие чего не могут быть усилены фильтром. Их импульсные характеристики равны d(n). В соответствии с (9.7) и (9.26) можно оценить вклад отдельных источников шума как

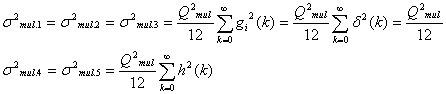        (9.27).

Дисперсия суммарного шума квантования на выходе фильтра в соответствии с (9.26) будет равна

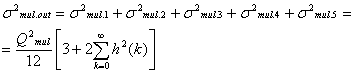        (9.28).

            Общая ошибка квантования , обусловленная квантованием входного сигнала и квантованием произведений , определяется суммой оценок соответствующих ошибок.

При суммировании чисел с фиксированной точкой ошибка округления не возникает (если только сумматор имеет разрядность не меньше разрядности слагаемых). Однако, при суммировании чисел с фиксированной разрядностью возможно возникновение переполнения, когда получившийся результат не помещается в количество разрядов, соответствующее разрядности слагаемых. При возникновении переполнения воизбежание нарушения алгоритма функционирования фильтра сумма должна быть ограничена с учетом знака на уровне максимального значения, умещающегося в заданное количество разрядов результата. При программной реализации фильтра это осуществляется соответствующим ветвлением алгоритма функционирования, а при аппаратной реализации требует включения в схему фильтра специальных устройств анализа переполнения и ограничения суммы с учетом знака. Однако, даже реализация указанных средств не решает всех проблем, связанных с переполнением, так как при наличии переполнений фильтр превращается в существенно нелинейное устройство со всеми вытекающими из этого последствиями. Поэтому, для нормальной работы фильтра необходима реализация специальных мер, позволяющих избежать появления ситуации переполнения вообще.

Одно из средств для предотвращения переполнения заключается во введении масштабирования, которое сводится к сдвигу вправо (что эквивалентно делению) двоичных кодов слагаемых на всех входах сумматоров. Если исходные слагаемые нормированы на уровне 1.0, то при суммировании двух чисел, для исключения возможности переполнения необходимо каждое из слагаемых сдвинуть на один разряд вправо, что эквивалентно делению каждого слагаемого на 2. После этого, каждое из слагаемых по модулю не будет превышать 0.5, а, значит, их сумма не превысит 1.0. Если у сумматора больше двух входов, то слагаемые должны быть сдвинуты на большее количество разрядов. Такой метод называется автоматическим масштабированием.

В результате такого масштабирования возникает ошибка масштабирования, связанная с тем, что младший разряд (или разряды при сдвиге более чем на один разряд) сдвигаемых слагаемых теряются и результирующая ошибка их представления увеличивается. Так, при сдвиге слагаемых на один разряд максимальное значение ошибки масштабирования равно

                                       (9.29),

где b – количество разрядов в представлении слагаемого. Если сдвигаемое слагаемое представляет собой число со знаком в прямом коде, то возможные значения этой ошибки равны 2^-b, -2^-b, 0. Если принять

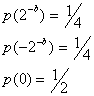                                                             (9.30),

то эта ошибка может быть представлена как случайный шум со средним значением равным 0 и дисперсией

                                                                 (9.31).

Если слагаемое представляет собой число в дополнительном коде, то ошибка масштабирования может принимать значения -2^-b или 0 с равной вероятностью 0.5. При этом шум масштабирования имеет среднее значение -2^-b/2 и дисперсию

                                                     (9.32).

Таким образом ошибки масштабирования могут быть учтены в модели фильтра аналогично ошибкам квантования.

            Другой способ предотвращения возможности переполнения сводится к масштабированию входных сигналов фильтра или его составных частей. Если импульсная характеристика фильтра или некоторой его части равна h_i(n), то выходной сигнал фильтра (или его части) y_i(n) ограничен величиной

                                          (9.33),

где - верхняя граница входного сигнала фильтра. Если , то необходимым условием отсутствия переполнения является

                                                               (9.34).

Если коэффициенты фильтра заданы (т.е. заданы h_i(n)), то, для того чтобы не было переполнений, т.е. чтобы выходной сигнал любого сумматора не превышал единицы, необходимо соответствующим образом ограничить величины входного сигнала и выходных сигналов умножителей. С этой целью вводится такое масштабирование, чтобы сигналы

                                (9.35),

где g_i – масштабирующие коэффициенты.

            Масштабирующие умножители включают на входах фильтра или на выходах умножителей. Если , то достаточным условием отсутствия переполнений является согласно (9.35) выбор масштабирующих коэффициентов исходя из условия

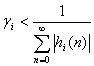                                                             (9.36).

Коэффициенты g_i выбирают, как и в случае автоматического масштабирования, обычно равными степеням двойки, и масштабирующее умножение сводится к сдвигам. При этом, аналогично случаю автоматического масштабирования, возникает шум масштабирования, который снижает отношение сигнал-шум на выходе фильтра.

            При существенном уменьшении амплитуд сигналов, проходящих через фильтр, уменьшается отношение сигнал-шум на выходе фильтра. Вычисление масштабирующих коэффициентов по формуле (9.36) часто приводит к завышенным результатам и, следовательно, к уменьшению эффективности работы фильтра. Помимо этого, при сложных структурах фильтра вычисление суммы бесконечного ряда отсчетов импульсной характеристики фильтра может оказаться сложно реализуемым. Поэтому расчет масштабных коэффициентов часто реализуют по другой методике, основанной на анализе спектра входного сигнала и частотных свойств фильтра.

            Если структура фильтра содержит m сумматоров, то выходной сигнал i-го сумматора vi(n) можно представить в виде

                                           (9.37),

где x(n) – входной сигнал фильтра, h_i(n) – импульсная характеристика части фильтра от входа до выхода i-го сумматора.

Z-преобразование сигнала  v_i(n) можно записать как

                                                     (9.38),

где H_i(z) – передаточная функция части фильтра от входа до выхода i-го сумматора.

            Частотную характеристику сигнала v_i(n) (для устойчивого фильтра) можно получить сделав в выражении (9.38) замену переменных

                                      (9.40).

Тогда сам выходной сигнал сумматора v_i(n) можно определить как обратное преобразование Фурье от V_i(e^jwT)

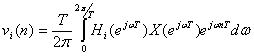                                 (9.41).

            Если сделать предположение о том, что модуль спектра входного сигнала x(n) ограничен некоторой величиной C, то можно оценить максимальное значение модуля выходного сигнала сумматора

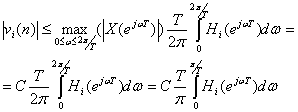                      (9.42).

            Если входной сигнал фильтра x(n) подвергается предварительному масштабированию на коэффициент l_i, то последнее выражение принимает вид

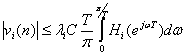                                     (9.43).

            Для исключения переполнений на выходе сумматора, т.е. для выполнения условия  достаточно выбрать значение нормирующего множителя l_i таким, что

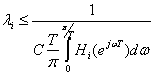                                             (9.44).

Если сделать предположение о том, что модуль частотной характеристики H_i(e^jwT) ограничен некоторой величиной D, то можно сделать  оценку максимального значения модуля выходного сигнала сумматора другим способом, а именно

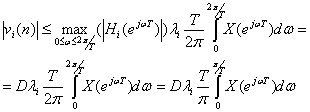                  (9.45).

В этом случае нормирующий множитель l_i для исключения переполнения на выходе  сумматора может быть выбран таким, что

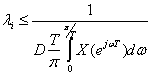                                              (9.46).

Наконец, применив к выражению (9.41) неравенство Коши-Буняковского () можно получить следующее неравенство

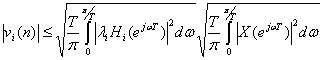               (9.47).

Если предположить, что энергия спектра входного сигнала (второе подкоренное выражение в неравенстве (9.47)) ограничена некоторой величиной E, то нормирующий множитель l_i может быть выбран исходя из следующего выражения

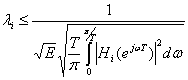                                     (9.48).

Все три варианта выбора масштабирующего множителя базируются на наличии  достоверной информации о спектральных характеристиках входного сигнала фильтра. Если эта информация не является абсолютно достоверной, то вероятность возникновения переполнения на выходе сумматора не является нулевой.

            Для исключения переполнения на выходах всех сумматоров, входящих в структурную схему фильтра необходимо сделать оценку коэффициентов l_i для каждого из сумматоров и выбрать окончательное значение нормирующего коэффициента на входе фильтра как

                                               (9.49).

            Как и в случае автоматического масштабирования, коэффиценты l выбирают обычно равным степеням числа 2, что превращает операцию масштабирующего умножения в сдвиг кода входного сигнала на соответствующее число разрядов вправо.

            Масштабирующий умножитель, как и любой другой умножитель в структурной схеме фильтра является источником шума ошибки квантования, влияние которого на выходной сигнал может быть учтено аналогично шумам других умножителей.

            Очевидно, что в случаях, когда некоторый сумматор в структурной схеме фильтра складывает больше двух слагаемых, даже при отсутствии переполнения в конечной сумме, оно может иметь место в промежуточных частичных суммах. Этот факт не был учтен в предыдущих рассуждениях. Однако, если входные и промежуточные цифровые сигналы фильтра представлены в дополнительном коде, то все вышеприведенные методы нормирования остаются правомерными, поскольку при суммировании чисел в дополнительном коде, конечный результат остается правильным (при отсутствии в нем переполнения) даже при наличии переполенния в частичных суммах.

            Предыдущий анализ базировался на предположении о том, что сигналы шумов статистически независимы от выборки к выборке и от источника к источнику. Это справедливо если разность между двумя соседними отсчетами входного сигнала значительно больше шага квантования. Ясно, что во многих случаях (в частности, когда входной сигнал постоянен или равен нулю) такое предположение несправедливо. При этих обстоятельствах ощибки квантования могут быть сильно коррелированы. Это может привести к нарушению нормальной работы фильтра, в результате чего фильтр становится неустойчивым, а на его выходе генерируются установившиеся периодичесткие колебания. Этоя явление называется эффектом мертвой зоны, а периодические колебания на выходе называются колебаниями предельного цикла. Общий анализ этого нелинейного эффекта довольно сложен. Поэтому проведем исследование данного явления для простейших цифровых фильтров.

            Рассмотрим фильтр первого порядка, описываемый разностным уравнением

                                         (9.50).

Передаточная функция такого фильтра имеет вид

                                          (9.51).

Структурная схема фильтра представлена на рис.9.6.

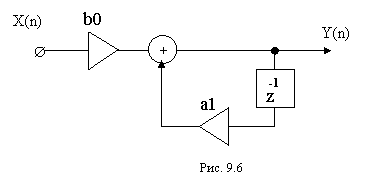Импульсная характеристика такого фильтра равна

                                                            (9.52).

            Если коэффициент a₁ равен 1 или –1, то фильтр становится неустойчивым и имеет импульсную характеристику

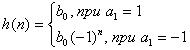                                    (9.53).

            В таблице 9.1 представлены точные значения отсчетов импульсной характеристики (9.52) при b₀=10, a₁=0.9.

n	h(n)	HQ(n)
0	10	10
1	9	9
2	8.1	8
3	7.29	7
4	6.561	6
5	5.9049	5
6	5.31441	5
…	…	…
100	2.65614*10^-4	5

            Теперь предположим, что фильтр имеет десятичный умножитель с фиксированной точкой, в котором каждое произведение a₁*y(n-1) округляется до ближайшего целого согласно условию

                                   (9.54).

В третьем столбце таблицы 9.1 представлены отсчеты импульсной характеристики такого фильтра. Как видно, при отклик фильтра становится постоянным, и квантование делает фильтр неустойчивым.

Если предположить, что разностное уравнение (9.50) остается справедливым для неустойчивого фильтра, то эффективное значение a₁ должно быть равно 1 при a₁>0 или –1 при a₁<0. Если это имеет место, то

                                          (9.55).

Это значит, что

                                         (9.56),

или                                (9.57).

Это равенство выполняется при условии, что

                                            (9.58).

Поэтому фильтр будет устойчивым, если

                                                (9.59).

            Поскольку y(n-1) – целое число, то фильтр будет устойчивым при . Если , то отклик фильтра будет затухать при отсутствии входного сигнала пока выходной сигнал не достигнет зоны [-k,k], называемой мертвой зоной. Когда это произойдет, режим фильтра станет неустойчивым. Любая причина, обуславливающая превышение модулем выходного сигнала величины k, приводит к восстановлению устойчивости. Однако, при отсутствии входного сигнала отклик снова затухает до величины, соответствующей мертвой зоне.

            Таким образом, фильтр будет находиться в режиме в режиме предельного цикла с амплитудой выходного сигнала равной k. Поскольку эффективное значение a₁ равно 1 при a₁>0 или –1 при a₁<0, то частота такого предельного цикла равна 0 или w_s/2.

            Если в фильтре используется двоичный умножитель с шагом квантования результата равным q, то условие появления колебаний предельного цикла имеет вид

                                                       (9.60).

Это выражение может быть использовано для выбора минимального количества разрядов вычислительного устройства из условия ограничения амплитуды колебаний предельного цикла на заданном уровне.

            Проведем анализ эффекта мертвой зоны для фильтра второго порядка, который описывается разностным уравнением

                       (9.61),

и имеет передаточную функцию

               (9.62).

            Если полюсы фильтра комплексные, то импульсная характеристика такого фильтра описывается выражением

                                        (9.63),

где      

                                 (9.64).

При a₂=1 импульсная характеристика имеет вид синусоиды с постоянной амплитудой и частотой равной

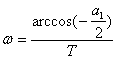                                                       (9.65).

Поэтому, квантование произведений будет приводить к неустойчивости, если эффективное значение a₂ будет равно 1. При этом

                                         (9.66).

Следовательно, как и ранее условие неустойчивой работы фильтра можго определить как

                                               (9.67).

Если k – целое, то величины a₂ из диапазонов

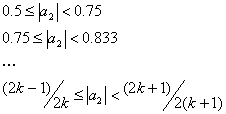                           (9.68)

будут приводить к появлению мертвых зон [-1,1], [-2,2], …, [-k,k] соответственно.

            Если в фильтре используется двоичный умножитель с шагом квантования результата равным q, то условие появления колебаний предельного цикла имеет вид

                                                      (9.69).