Лекция №7

«Z – преобразование»

 

 

            Z – преобразование является одним из математических методов анализа и проектирования дискретных систем.

Аппарат z-преобразования играет для цифровых систем ту же роль, что и преобразование Лапласа для непрерывных систем.

            Мотивировку использования z-преобразования для исследования дискретных систем можно пояснить на примере преобразования Лапласа квантованного сигнала. Если выходной сигнал идеального импульсного элемента fd(t) определен как

                                     (7.1),

то преобразование Лапласа для fd(t) определяется выражением

                                (7.2).

            выражение для Fd(p) не является рациональной функцией относительно p, поскольку содержит множитель e-Tp. Для упрощения анализа желательно преобразовать иррациональную функцию Fd(p) в рациональную посредством замены комплексной переменной p на другую комплексную переменную z. Выбор такой замены очевиден

                                                                                                (7.3).

При этом обратное соотношение имеет вид

                                                                                          (7.4).

В этих выражениях T – период квантования, z – комплексная переменная, действительная и мнимая части которой определяются как

                                                                              (7.5),

где

                                                                                        (7.6).

            Подставляя новую переменную z в выражение (7.2) получим

                                              (7.7),

что является рациональной функцией относительно z.

            Выражение (7.7) называется z-преобразованием функции f(t).

            Поскольку z-преобразование функции получается из ее преобразования Лапласа, то в общем для любой функции f(t), имеющей преобразование Лапласа, существует также и z-преобразование.

            Процедура нахождения z-преобразования непрерывной функции f(t) включает следующие этапы:

-        определение fd(t) как выходного сигнала идеального импульсного элемента для входной функции f(t);

-        определение преобразования Лапласа fd(t)

;

-        замена eTp на z  в выражении для Fd(p), чтобы получить

.

            Выражение (7.7) используется для нахождения z-преобразования функции f(t). Однако неудобство этого выражения состоит в том, что оно является бесконечным рядом, а не эквивалентной функцией в компактной форме.

            Альтернативное выражение для z-преобразования функции можно получить, если использовать ее изображение F(p) и теорему о вычетах. Так, если функция f(t) имеет изображение F(p), которое представимо в виде

                                                                                                (7.8),

то z-преобразование этой функции можно найти в виде

                                                                        (7.9),

где xn – простые полюса функции F(p), k – число этих полюсов.

Если F(p) имеет кратные полюсы p1, p2, …, pk с кратностью m1, m2, …, mk соответственно, тоz-преобразование F(p) можно найти в виде

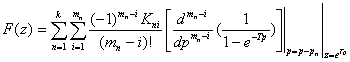                                (7.10),

где

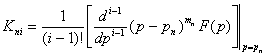                                                     (7.11).

            Проектирование непрерывных систем часто основывается на анализе распределения нулей и полюсов передаточной функции системы на плоскость комплексной переменной p. Аналогично, полюсы и нули z-преобразования передаточной функции определяют реакцию системы в моменты дискретизации. Поэтому важно определить сответствие между плоскостью комплексной переменной p и плоскостью комплексной переменной z.

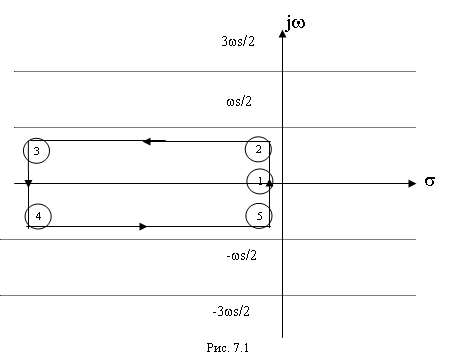
            Как было установлено ранее, преобразование Лапласа дискретной функции fd(t) является переиодической функцией с периодом jws, где ws – частота дискретизации. В соответствии с этим плоскость комплексной переменной p можно разделить на бесконечное число периодических полос (рис.7.1).

Основная полоса расположена в диапазоне частот от -ws/2 до +ws/2, а дополнительные полосы расположены в диапазоне от -ws/2 до -3ws/2, от -3ws/2 до -5ws/2 и т.д. для отрицательных частот и от ws/2 до 3ws/2, от 3ws/2 до 5ws/2 и т.д. для положительных частот. Если рассматривать только основную полосу, то контур 1-2-3-4-5-1, расположенный в левой половине p-плоскости, отображается преобразованием z=eTp в единичную окружность на z-плоскости с центром в начале координат (рис.7.2).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


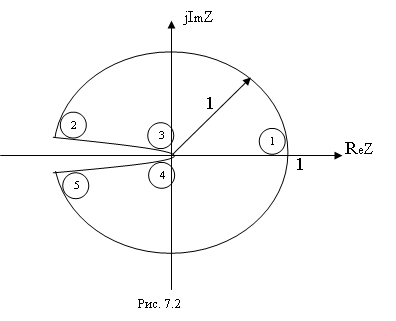
            Так как

                                                                         (7.12)

для целых n, то все другие дополнительные полосы в левой половине p-плоскости отображаются в тот же самый единичный круг на z-плоскости. Все точки левой половины p-плоскости отображаются внутрь единичного круга на z-плоскости. Точки правой половины p-плоскости отображаются  в области вне единичного круга на z-плоскости.

            Линии постоянного затухания, описываемые на p-плоскости уравнением s=s1 отображаются на z-плоскости в окружность с радиусом  и с центром в начале координат (рис.7.3).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


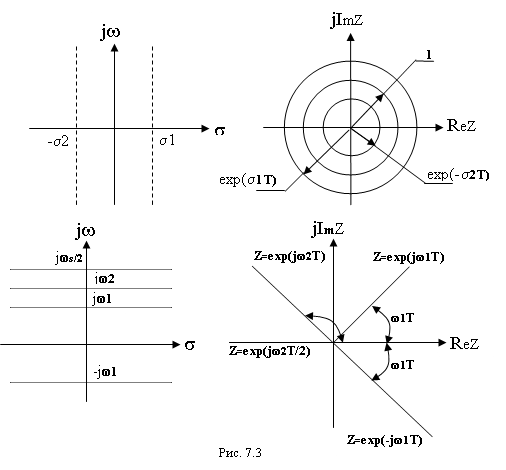
Линии постоянной частоты, описываемые на p-плоскости уравнением w=w1 отображаются в луч, исходящий из начала координат под углом w1T радиан. Угол измеряется от положительного направления действительной оси.

            Преобразование Лапласа и его обратное преобразование являются однозначными, т.е. если F(p) есть преобразование Лапласа для функции f(t), то f(t) является обратным преобразованием Лапласа для функции F(p). Для z-преобразования обратное z-преобразование не является однозначным. Корректный результат обратного z-преобразования функции F(z) есть f(kT), которая равна f(t) только в моменты квантования t=kT.

            В общем случае обратное z-преобразование может быть определено одним из следующих методов.

            Метод разложения на простые дроби. Известно, что z-преобразованием для функции f(kT)=Ae-akT является функция Az/(z-e-aT). Таким образом, если удастся представить функцию F(z) в виде

                                                                              (7.13),

то функция f(kT), которая является обратным z-преобразованием для функции F(z) будет иметь вид

                                                                        (7.14).

Следуя данному методу необходимо:

-        разложить на простые множители функцию F(z)/z;

 

                                                      (7.15),

-         умножить обе части получившегося выражения на z

 

                                                      (7.16),

-        записать выражение для обратного z-преобразования как сумму отдельных составляющих, каждая из которых соответствует своему слагаемому в выражении для F(z).

Метод разложения в степенной ряд. Из (7.7) следует, что

                       (7.17).

Следоватеельно, коэффициенты ряда соответствуют значениям f(t) в моменты квантования. Таким образом, из записи ряда можно получить выражение для f(kT).

            Формула обратного z-преобразования. Обратное z-преобразование можно получить с помощью формулы

                                                                             (7.18),

где G - замкнутый контур на z-плоскости, включающий все особые точки   F(z)zk-1. При этом значение интеграла можно найти по теореме вычетов

                                                                               (7.19)

в полюсах F(z).

            Свойства z-преобразования.

1.     Суммирование и вычитание. Если

            то                                                    (7.20).

2.     Умножение на константу. Если

, то

                                                       (7.21),

            где a – константа.

3.     Сдвиг во временной области. Если , то

                                            (7.22),

            где n – положительное целое число.

4.           4. Смещение в области изображений. Если , то

                                              (7.23),

            где a – константа.

5.     Теорема о начальном значении. Если  и если существует предел , то

                                                 (7.24),

т.е. значение дискретного сигнала f(t) при

 t=0 определяется значением F(z) при z=¥.

6.     Теорема о конечном значении. Если  и если функция  не имеет полюсов на окружности единичного радиуса и вне ее, то

                                    (7.25).

7.     Теорема о свертке во временной области. Если  и f1(t)=f2(t)=0 при t<0, то

                    (7.26).

            Выражение () называется сверткой во временной области.

            Поскольку метод z-преобразования при анализе дискретных систем аналогичен методу преобразования Лапласа при анализе непрерывных систем, необходимо найти способ описания дискретной системы в терминах z-преобразования.

            Для линейной непрерывной системы (рис.7.4)

 

 

 


 

 

 

 

отношение между непрерывным выходным сигналом с(t) и непрырывным входным сигналом r(t) описывается передаточной функцией

                                                                                                 (7.27),

где R(p) и C(p) – преобразования Лапласа входного и выходного сигнала системы соответственно. Преобразует эту системы в дискретную, установив на входе и на выходе ее синхронизированные импульсные элементы (рис.7.5).

 

 

 


           

 

 

 

Если ко входу линейной системы приложен дискретный сигнал rd(t), то выходной сигнал системы можно записать в форме

                                   (7.28),

где g(t) – переходная функция системы.

При t=kT, где k – положительное целое число, это выражение примет вид

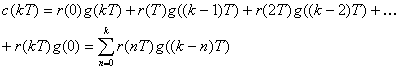        (7.29).

Беря z-преобразование от обеих частей последнего выражения и применяя теорему о свертке во временной области, получим

                                                                                            (7.30),

где

                                                   (7.31)

называется импульсной передаточной функцией линейной дискретной системы.

            При последовательном соединении двух дискретных систем с импульсными передаточными функциями G1(z) и G2(z), частота дискретизации которых одинакова, а моменты дискретизации синхронизированы, импульсная передаточная функция системы в целом равна произведению импульсных передаточных функций этих систем

                                                                                         (7.32).

            Экстраполятор нулевого порядка имеет передаточную функцию

                                                                                        (7.33).

Z-преобразование этой функции, а следовательно импульсная передаточная функция экстраполятора нулевого порядка равна

                                                                        (7.34).

Этот результат очевиден, так как экстраполятор нулевого порядка в течение периода квантования удерживает постоянным дискретный сигнал, полученный в результате дискретизации, и вычисление z-преобразования для передаточной функции фиксатора должно определять исходный дискретный сигнал. Однако в большинстве случаев на практике за экстраполятором нулевого порядка следует непрерывная часть системы (рис.7.6).

 

 

 

 

 

 

 


Z-преобразование выходного сигнала такой системы равно

                                                                                          (7.35),

где

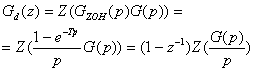                                                         (7.36).

В данном случае z-преобразование числителя передаточной функции экстраполятора нулевого порядка можно вынести за скобки в соответствии с теоремой о сдвиге во временной области (7.22), однако z-преобразование G(p)/p должно быть определено как для одного целого.

            Теоретически при бесконечном возрастании частоты квантования дискретная система стремится к соответствующей аналоговой системе. Однако, это не означает, что

                                                                                            (7.37).

            Так как z-преобразование основано на амплитудно-импульсной модуляции, то устремление T к нулю лишено физического смысла. Другими словами, если сигнал r(t) поступает на импульсный элемент, выходным сигналом которого является rd(t), то устремление переиода квантования к нулю не обеспечивает совпадение r(t) и rd(t). Это объясняет, почему выражение (7.37) в общем случае не справедливо. Однако если дискретный сигнал rd(t) подать на вход экстраполятора нулевого порядка, выходным сигналом которого является сигнал hd(t), то при устремлении периода дискретизации к нулю справедливо соотношение

                                                                                               (7.38),

или

                                                                                            (7.39).

            Таким образом, если непрерывный сигнал послан на идеальный импульсный элемент с экстраполятором нулевого порядка, то выходной сигнал последнего совпадает с исходным непрерывным сигналом при устремлении периода дискретизации к нулю.