Лекция №2

«Дискретные и цифровые системы. Временная дискретизация»

 

            Системы обрабатывают сигналы, приходящие на них и, в результате этого вырабатывают соответствующие выходные сигналы с целью выполнения закона управления. В зависимости от того, сигналы какого типа используются в системе, последние подразделяются на непрерывные и дискретные системы.

            Работа непрерывных систем описывается соответствующими системами дифференциальных уравнений типа:

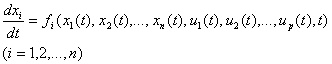             (2.1).

где x1(t), x2(t), …, xn(t) – переменные состояния системы, u1(t), u2(t), …, up(t) – входные сигналы, fi – функциональные соотношения, которые в общем случае могут быть линейными или нелинейными.

            Система, в которой используются дискретные сигналы, называется дискретной  системой. Дискретные автоматические системы подразделяются на импульсные, релейные и цифровые.

            Автоматическая система называется импульсной, если хотя бы один сигнал в ней дискретизируется по времени.

            Автоматическая система называется релейной, если хотя бы один сигнал в ней квантуется по уровню.

            Автоматическая система называется цифровой, если хотя бы один сигнал в ней дискретизируется по времени и квантуется по уровню.

            Микропроцессорная автоматическая система это цифровая система, алгоритм функционирования которой полностью или частично реализован программно с помощью средств микропроцессорной техники. Таким образом, микропроцессорные системы являются подклассом цифровых систем. Характерными особенностями микропроцессорных систем являются:

-        вычислительное запаздывание реакции системы связанное с последовательным выполнением программного алгоритма функционирования и конечным быстродействием микропроцессорной техники;

-        распределение функций системы между ее аппаратной и программной частями.

Цифровые системы, в свою очередь, являются подклассом импульсных систем, характерной чертой которого является квантование сигналов по уровню и, связанные с ним, динамические и точностные особенности работы систем.

            Обобщенная структурная схема импульсной системы, управляющей непрерывным объектом, может быть представлена в виде последовательного соединения импульсного элемента и непрерывной части (рис.2.1).

 

 

 

 

 

 

 

 


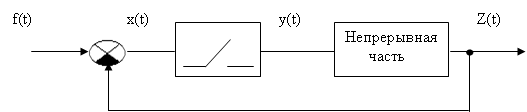
Обобщенная структурная схема микропроцессорной автоматической системы представлена на рис.2.2.

 

 

 

 

 

 

 

 

 

 

 

 


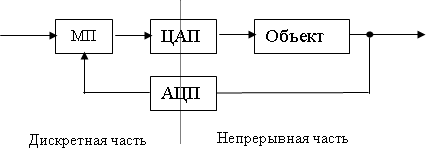
Микропроцессор (МП) играет роль задающего, сравнивающего и управляющего устройства. Аналоговые сигналы, соответствующие переменным состояния объекта с помощью аналого-цифрового преобразователя (АЦП) преобразуются в цифровые. Т.о., АЦП играет роль импульсного элемента и квантователя по уровню. Выработанные МП цифровые сигналы управления, с помощью цифро-аналогового преобразователя (ЦАП) преобразуются в аналоговые, и в таком виде подаются на управляемый объект. В преобразовательной технике часто оконечное исполнительное устройство автоматической системы имеет импульсные сигналы управления, вследствие чего ЦАП может быть заменен на цифровой импульсный модулятор.

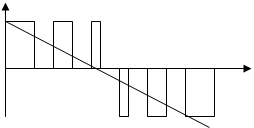
Сущность импульсного элемента заключается в преобразовании входного аналогового сигнала в выходной импульсный сигнал, что осуществляется модуляцией некоторой последовательности импульсов входным аналоговым сигналом. В зависимости от вида модуляции различают широтно-импульсные и амплитудно-импульсные системы. В широтно-импульсных системах модулируемым параметром является длительность импульсов при постоянных их амплитуде и частоте (рис.2.3).

 

 

 

 

 

 

 

 

 


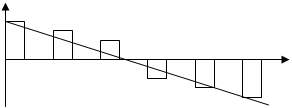
В амплитудно-импульсных системах модулируемым параметром является амплитуда импульсов при постоянных их частоте и длительности (рис.2.4).

 

 

 


 

 

 

Микропроцессорные автоматические системы можно отнести к амплитудно-импульсным системам с учетом эффекта квантования по уровню. Аналогом модулируемой амплитуды импульсов является величина двоичного кода. Поэтому в дальнейшем будем рассматривать амплитудно-импульсные системы с учетом вышеуказанных особенностей.

В амплитудно-импульсной системе выходным сигналом импульсного элемента является последовательность импульсов, амплитуда которых пропорциональна значению входного аналогового сигнала ошибки x(t) в дискретные моменты времени t=mT, где T – называется периодом дискретизации. Т.о. импульсная система реагирует лишь на дискретные значения ошибки  при t=mT

                                          (2.2)

и не реагирует на изменение внешнего воздействия f(t) и выходной переменной системы z(t) между этими дискретными моментами времени.

            В амплитудно-импульсных системах выходной сигнал импульсного элемента является периодической последовательностью импульсов определенной формы, амплитуда которых пропорциональна дискретным значения входной величины x(mT).

            Назовем идеальным импульсным элементом такой, выходной сигнал которого X*(t) представляет собой последовательность d-функций, модулированных дискретными значениями входной величины x(mT).      Т.о. модулируемая последовательность импульсов идеального импульсного элемента может быть описана уравнением

                                                                                       (2.3).

Она изображена на рис.2.5.

 

 

 

 

 

 

 


Модуляция заключается в том, что площади импульсов данной последовательности становятся равными дискретным значениям входной величины x(mT). Очевидно, что любой реальный импульсный элемент с произвольной формой импульсов может быть представлен в виде последовательного соединения идеального импульсного элемента и некоторой непрерывной формирующей цепи, реакция которой на импульсное воздействие равна s(t). Если обозначить через s(p) преобразование Лапласа функции s(t), то структурная схема произвольного импульсного элемента примет вид, изображенный на рис.2.6.

 

 

 


           

 

 

 

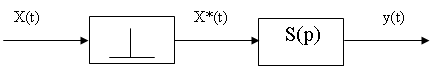
Рассмотрим вначале работу идеального импульсного элемента. В свете вышеизложенного ясно, что если входной сигнал f(t)=0 при , то выходной сигнал идеального импульсного элемента может быть представлен в виде

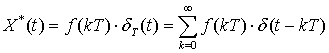                                      (2.4)

Найдем преобразование Лапласа функции X*(t).

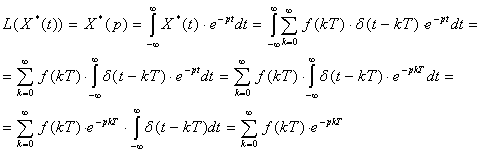
Итак,

                                         (2.5)

Это выражение определяет отношение между решетчатой функцией x(kT) и ее изображением и называется дискретным преобразованием Лапласа.

            Функцию dT(t) как периодическую функцию можно представить в виде разложения в ряд Фурье

                                                                                    (2.6),

где  - частота дискретизации, Ck – коэффициенты ряда Фурье, определяемые по формуле

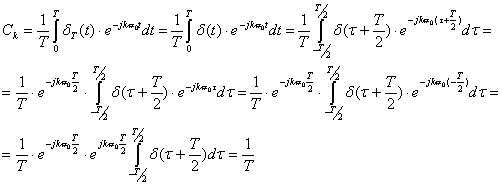
Итак, имеем

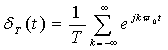                                                                              (2.7).

Найдем теперь другой вид функции X*(p)

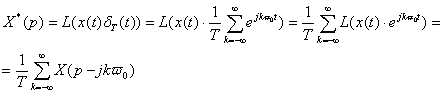         (2.8)

Это соотношение устанавливает связь между изображениями непрерывной функции X(p) и соответствующей ей решетчатой функции X*(p).

            Подстановкой p=jw перейдет от преобразования Лапласа к преобразованию Фурье

                                                                      (2.9).

Величина X*(jw) называется спектром выходной величины импульсного элемента X*(t). Заменим в этом выражении w на , где r – целое число

                                ,

теперь введем новую переменную

            .

Т.о., получаем

                                                                            (2.10).

Формула (2.10) означает, что спектр выходного сигнала идеального импульсного элемента является периодической функцией частоты с периодом, равным частоте квантования w0.

            Предположим, что входной сигнал идеального импульсного элемента имеет спектр, изображенный на рис.2.7.

Тогда, в соответствии с вышеизложенным, выходной сигнал идеального импульсного элемента будет иметь спектр, представленный на рис.2.8.


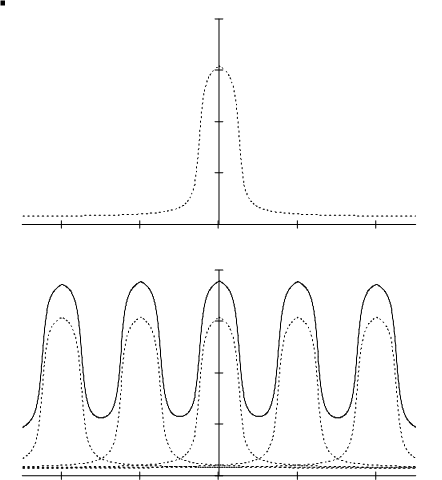
Из рисунка видно, что дискретизация по времени вносит искажения в исходный сигнал, выражающиеся в том, что более верхние частоты суммируются с более низкими частотами, и в результате этого исходная форма спектра меняется. Этот эффект называется наложением спектров. Он влечет за собой частичную или полную потерю информации о исходном сигнале. После такой дискретизации исходный сигнал уже никогда не сможет быть восстановлен в полном объеме.

            Выясним условия, при которых дискретизация по времени не приводит к потере информации о сигнале. Как видно из рис.2.8, если спектр исходного непрерывного сигнала X(jw) не ограничен (или не финитен), то искажения будут иметь места всегда. Поэтому предположим, что спектр X(jw) финитен, т.е. X(jw)=0 при , где wc – частота среза (рис.2.9).

 


 

На рис.2.10 представлен результирующий спектр выходного сигнала идеального импульсного элемента при условиях: w0<2wc (а), w0=2wc (б), w0>2wc (в).


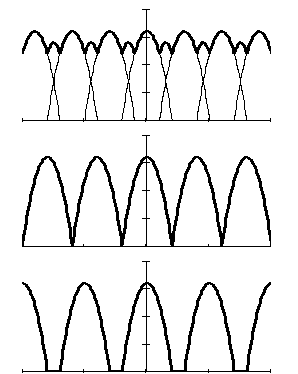
При w0>2wc происходит наложение смещенных спектров и в результате X*(jw) даже в диапазоне частот (-w0/2, w0/2) отличается от X(jw). При w0>2wc и w0=2wc наложение смещенных спектров отсутствует и в диапазоне (-w0/2, w0/2) X*(jw) и X(jw) по форме совпадают и различаются лишь масштабом на множитель 1/T. Если такой дискретный сигнал X(nT) пропустить через идеальный фильтр низкой частоты, амплитудно-частотная характеристика которого представлена на рис.2.11, то на выходе получим восстановленный непрерывный сигнал x(t). Определим формулу восстановления.

 

 

 

 

 

 

 

 

 

 

 


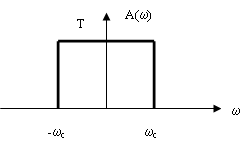
Из рис.2.11 видно, что частотную характеристику требуемого низкочастотного фильтра можно записать как

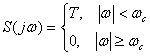                                                                                  (2.11).

При условии  изображение выходного сигнала идеального импульсного элемента можно записать как

                                    .

Переходя к спектрам, получим

                                    .

Найдем y(t) по формуле обратного преобразования Фурье

           

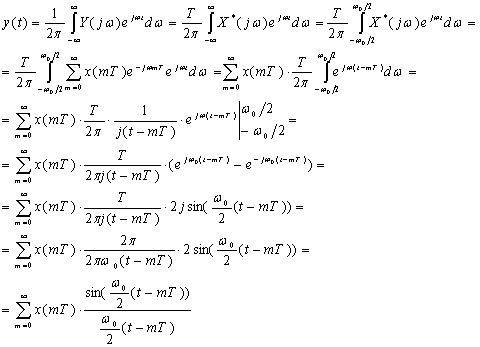
Итак, имеем

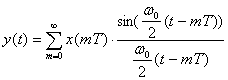                                                               (2.12).

Все вышесказанное суммируется в фундаментальной теореме дискретизации, которая называется еще теоремой Котельникова. Она звучит следующим образом:

            Непрерывный сигнал, обладающий финитным спектром, ограниченным частотой среза wc однозначно представляется своими значениями в равноотстоящих точках, если частота квантования w0 больше или равна 2wc. При этом непрерывный сигнал может быть получен из дискретного по интерполяционной формуле (2.12).


            На практике основная трудность заключается в том, что реальные непрерывные сигналы практически никогда не обладают финитным спектром, т.е., спектр этих сигналов не равен нулю вне полосы частот (-w0/2, w0/2). Это приводит к тому, что на вход импульсного элемента поступают гармонические составляющие, не удовлетворяющие теореме Котельникова. Эти составляющие не могут быть корректно обработаны импульсным элементом. Поэтому, та часть выходного сигнала импульсного элемента, которая относится к этим гармоническим составляющим представляет из себя ни что иное, как  шум дискретизации, искажающий полезный сигнал. Это искажение может быть проиллюстрировано на примере явления т.н. «наложения частот» (рис.2.12). Пусть гармонический сигнал с частотой 8 Гц дискретизируется с частотой 10 Гц.

 

 

Из рис.2.12 видно, что дискретные отсчеты, получившиеся в результате такой дискретизации нельзя отличить от дискретных отсчетов гармонического сигнала с частотой 2 Гц. Такой эффект, называемый «наложением частот» наблюдается для двух любых гармонических сигналов с частотами f1 и f2 соответственно, когда хотя бы одна из этих частот не соответствует теореме Котельникова и выполняется соотношение , где f0 – частота дискретизации.

            Для того, чтобы избежать искажения дискретного сигнала гармоническими составляющими входного аналогового сигнала, не соответствующими теореме Котельникова, все эти высшие гармонические составляющие должны быть отфильтрованы входным аналоговым фильтром до поступления сигнала на вход импульсного элемента. На практике отфильтровать все высшие гармонические составляющие не представляется возможным т.к., в этом случае фильтр должен был бы иметь прямоугольный вид амплитудно-частотной характеристики (рис.2.11), что недостижимо. Поэтому, часть шума дискретизации все-таки поступает на вход системы, ухудшая ее точностные характеристики. Качество фильтрации шума дискретизации зависит от порядка предварительного фильтра и его полосы пропускания.

            Выходные сигналы дискретной (в том числе и цифровой) системы управления перед подачей на управляемый объект должны быть вновь преобразованы в непрерывные. Это объясняется тем, что большинство систем управления спроектированы в расчете на непрерывные сигналы управления, и подача на них дискретных сигналов будет приводить к чрезмерному износу аналоговых элементов этих систем.

            Процесс восстановления аналоговых сигналов по их дискретным выборкам называется экстраполяцией. Существует несколько способов экстраполяции. На рис.2.10 представлен спектр дискретного сигнала F*(jw). Из рисунка видно, что для полного восстановления аналогового сигнала дискретный сигнал должен быть пропущен через идеальный низкочастотный фильтр с амплитудной характеристикой, показанной пунктиром. В этом случае процесс экстраполяции соответствовал бы формуле (2.12)

                                    .

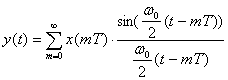Такой тип экстраполяции называется экстраполяцией Шеннона. Он имеет очень мало практического применения. Причиной этого является очень большая задержка сигнала между входом и выходом, характерная для этого метода. Действительно, в соответствии с (2.12), для того, чтобы точно восстановить значение аналоговой функции y(t)  в конечный момент времени t необходимо знать дискретные отсчеты x(mT) для m=0…¥. Т.о., этот метод экстраполяции может быть реализован лишь посредством запоминания большого числа отсчетов дискретной функции с последующим восстановлением аналоговой функции в соответствии с выражением (2.12). Он не применим в режиме реального времени. Кроме того, этот метод предполагает финитный спектр входного аналогового сигнала, чего реально практически не бывает.

            Неограниченность спектра реальных аналоговых сигналов приводит к тому, что точно восстановить такой сигнал по его дискретным выборкам невозможно. Можно лишь более или менее точно приблизить результирующий сигнал к его оригиналу.

            Для режима реального времени пригодны методы экстраполяции, позволяющие восстановить значения функции в моменты времени между двумя последовательными моментами дискретизации kT и (k+1)T на основании известных значений функции во все предшествующие моменты дискретизации kT, (k-1)T, (k-2)T, … и т.д. Известный метод экстраполяции основан на разложении искомой функции xa(t) в ряд на интервале между моментами дискретизации kT и (k+1)T

                      (2.13)

Для того, чтобы вычислить коэффициенты ряда (2.13) производные функции xa(t) должны быть получены в моменты выборки t=kT. Поскольку единственная доступная информация  об xa(t) – это ее значения в моменты выборки, то производные должны оцениваться по значения xa(kT). При малых периодах дискретизации с достаточной точностью первую производную можно заменить конечной разностью

                                                             (2.14).

Аналогично, вторую производную можно апроксимировать как

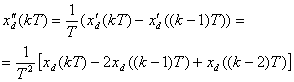                                              (2.15)

Отсюда видно, что чем выше порядок производной, тем болшее число предшествующих выборок нужно для ее апроксимации. Можно показать, что для апроксимации xa(n)(kT) необходима n+1 предшествующая выборка xa(kT). Накопление большого количества предшествующих выборок определяет большое временное запаздывание реакции системы. Это отрицательно сказывается на устойчивости системы. Поэтому на практике при экстраполяции по методу (2.13), как правило, ограничиваются одним или двумя начальными членами ряда. При сохранении только первого члена ряда уравнение экстраполяции имеет вид

                                                                                               (2.16).

Такой метод называется экстраполяцией нулевого порядка. При этом методе экстраполяции значение выходной величины неизменно втечение всего интервала дискретизации (рис.2.13).

 


 

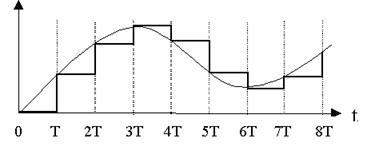
Как видно из рисунка, такой метод экстраполяции сопряжен с ошибкой, максимальное значение которой равно

                                     (2.17).

Оценим частотные свойства такой экстраполяции. Временную реакцию такого экстраполятора на импульсное воздействие можно описать уравнением

                        .

Эту функцию можно записать через единичную функцию

                                                                                       (2.18).

Переходя в область изображений, найдем передаточную функцию экстраполятора нулевого порядка

                                                                            (2.19).

Если подать на вход такого экстраполятора сигнал с выхода идеального импульсного элемента, то выходной сигнал экстраполятора можно вычислить как

                                     (2.20).

При подстановке p=jw получим

           

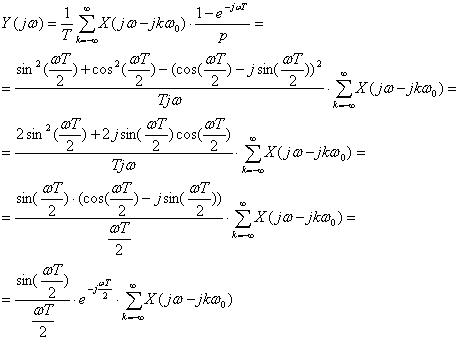
Итак, получим 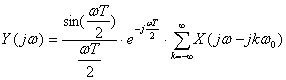                       (2.21)


Амплитудный спектр выходного сигнала экстраполятора нулевого порядка представлен на рис.2.14.

 

 

 

Из рисунка видно, что с помощью экстраполятора нулевого порядка не удается полностью восстановить исходный непрерывный сигнал, т.к. в спектре выходного сигнала присутствуют высшие гармоники, хотя и в уменьшенном виде. Точность экстраполятора нулевого порядка существенно зависит от частоты дискретизации w0. Функцию экстраполятора нулевого порядка на практике играет цифро-аналоговый преобразователь (ЦАП).

            При реализации двух начальных членов ряда (2.13) получим экстраполятор первого порядка (рис.2.15)

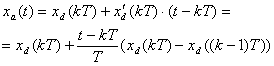                                       (2.22).

 

 

 

 

 

 

 

 

 

 

 

 

 

 


Ошибка экстраполяции первого порядка не будет превышать величину

                                                                         (2.23).

Выбор правильного значения периода дискретизации на практике зависит от свойств сигнала, метода восстановления и свойств системы. С одной стороны уменьшение периода дискретизации приводит к снижению ошибки отработки сигнала задания и уменьшению вычислительного запаздывания системы. Но, с другой стороны, это сопряжено с удорожанием системы из-за применения более быстродействующих АЦП, ЦАП и  микропроцессоров. Разумными критериями для выбора периода дискретизации могут служить величина рассогласования между исходным и восстановленным сигналами, а также, требуемая ширина полосы пропускания системы управления.

При отработке синусоидального сигнала с частотой w максимальные относительные ошибки восстановления вычисляются по формулам

                                                         (2.24)

для экстраполятора нулевого порядка, и

                                                                                     (2.25)

для экстраполятора первого порядка,

где N – количество интервалов дискретизации на периоде исходного сигнала.

Значения этих ошибок для некоторых, часто встречающихся значений N, представлены в табл.2.1.

 

Число отсчетов за период, N

Максимальная относительная ошибка, %

Эктраполятор 0 порядка

Эктраполятор 1 порядка

5

60

80

10

30

19

20

15

5

50

6

0.8

100

3

0.2

200

1.5

0.05

500

0.6

0.008

1000

0.3

0.002

 

            Если точность отработки сигнала задания не является превалирующим требованием, то величина периода дискретизации оценивается исходя из требуемой ширины полосы пропускания системы. Частота дискретизации в этом случае зависит от динамических свойств объекта управления и, как правило, может быть выбрана на уровне 10*Dw, где Dw - ширина полосы пропускания.