Лекция №13

«Цифровые регуляторы»

При проектировании как цифровой, так и аналоговой системы управления, ее основная задача заключается в обеспечении такого режима работы, при котором выходные параметры системы соответствуют входному сигналу задания. Традиционным методом обеспечения такого режима работы является использование обратной связи для образования сигнала ошибки между входным и выходным сигналами. Вычисленный сигнал ошибки обрабатывается регулятором, который на основе этого вырабатывает управляющий сигнал, поступающий на объект регулирования. Регулятор должен вырабатывать управляющий сигнал таким образом, чтобы свести сигнал ошибки между входным и выходным сигналами ошибки к нулю. При этом переходный процесс изменения сигнала ошибки должен удовлетворять определенным критериям качества. Таким образом обобщенная структурная схема системы управления имеет вид, представленный на рис.13.1.

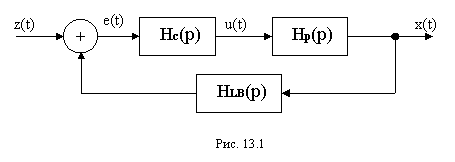
Здесь H_p(p) – передаточная функция объекта регулирования, H_c(p) – передаточная функция регулятора.

В цифровой системе управления вычисляемый сигнал ошибки является цифровым, а регулятор реализуется программно с помощью микропроцессора или аппаратно с помощью специального вычислительного устройства. Структурная схема цифровой системы управления представлена на рис.13.2.

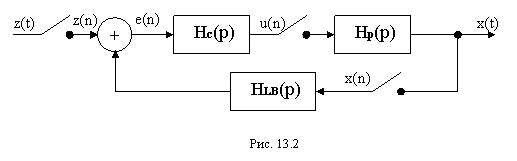
Импульсные элементы с экстраполяторами нулевого порядка на входе и выходе системы соответствуют аналогоцифровому и цифро-аналоговому преобразователям. На основании рис.13.2 можно определить импульсную передаточную функцию цифрового регулятора как

(13.1).

Отсюда

(13.2).

В аналоговых системах регулирования регуляторы, как правило, имеют передаточные функции фильтров нижних или верхних частот. В цифровых системах управления регуляторы реализуются с помощью цифровых фильтров.

Простейшими видами регуляторов являются классические П-, ПИ- и ПИД-регуляторы. Уравнение аналогового ПИД-регулятора имеет вид

(13.3),

где K – коэффициент усиления, T_I – постоянная времени интегрирования, T_D – постоянная времени дифференцирования. Структурная схема аналогового ПИД-регулятора представлена на рис.13.3.

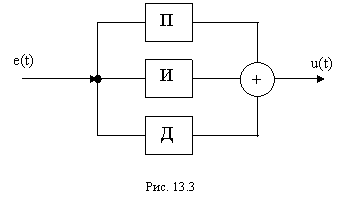
Для малых интервалов дискретизации T₀ это уравнение можно преобразовать в разностное с помощью замены производной первой разностью, а интеграла – суммой. Непрерывное интегрирование может быть заменено численным интегрированием по методу прямоугольников или трапеций. При использовании метода прямоугольников получим

(13.4).

Уравнение (13.4) представляет нерекуррентный алгоритм цифрового ПИД-регулятора. В нем для формирования суммы необходимо помнить все предыдущие значения сигнала ошибки e(t). Поскольку каждый раз значение управляющего сигнала u(n) вычисляется заново, такой алгоритм называется позиционным.

Запишем уравнение (13.4) для предыдущего момента дискретизации

(13.5).

Если теперь вычесть из уравнения (13.4) уравнение (13.5), то получим

(13.6).

Из уравнения (13.6) текущее значение управляющего сигнала можно вычислть как

(13.7),

где

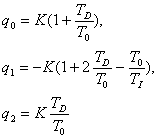(13.8).

В соответствии с уравнением (13.7) для вычисления нового значения управляющего сигнала необходимо помнить лишь прошлое значение управляющего сигнала и значения сигнала ошибки на текущем и двух предыдущих шагах дискретизации. Каждый раз вычисляется только приращение управляющего сигнала по сравнению с предыдущим его значением. Такой алгоритм называется скоростным. Уравнение скоростного алгоритма цифрового ПИД-регулятора представляет собой разностное уравнение цифрового фильтра со входным сигналом e(n) и выходным сигналом u(n). Структурная схема цифрового ПИД-регулятора, реализованного по такому алгоритму представлена на рис.13.4.

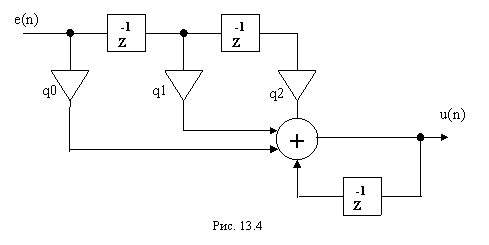
Если для аппроксимации интеграла использовать метод трапеций, то уравнение скоростного алгоритма цифрового ПИД-регулятора будет иметь вид, аналогичный (13.7), однако коэффициенты этого уравнения будут вычисляться по формулам

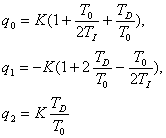(13.9).