Лекция №12

«Быстрое преобразование Фурье».

 

            Дискретное преобразование Фурье (ДПФ) периодического дискретного сигнала x(n) с периодом N  определяется как

                                   (12.1),

где  - основная частота преобразования (бин ДПФ).

Выражение (12.1) можно переписать в виде

                                                         (12.2),

где                                                                                            (12.3).

Коэффициент WN называется поворачивающим множителем. Легко показать, что  является периодической функцией с периодом N

                                   (12.4).

Поэтому ДПФ X(k) также является периодической функцией по аргументу k с периодом N.

            Дискретное преобразование Фурье может быть использовано и для представления сигнала x(n) конечной длины N, определенного при n=0,1,…,N-1 и равного нулю вне интервала [0,N-1]. Действительно, такой сигнал можно рассматривать как один период соответствующего периодического сигнала и сипользовать преобразования (12.2). Следует только считать, что вне интнрвала [0,N-1] X(k) и x(n) равны нулю.

            Если сравнить ДПФ конечного дискретного сигнала со спектром этого же сигнала, определяемым выражением

                                                                                (12.5),

то очевидно, что ДПФ представляет собой N отсчетов спектра, взятых на периоде с интервалом дискретизации по частоте, равным .

            В случае, когда x(n) является комплексным, при прямом вычислении N-точечного ДПФ нужно выполнить для каждого значения k (N-1) умножений и (N-1) сложений комплексных чисел или 4(N-1) умножений и 2(N-1) сложений действительных чисел. Для всех N значений k=0,1,…,N-1 требуется (N-1)2 умножений и N(N-1) сложений комплексных чисел. Для больших значений N (порядка нескольких сотен или тысяч) прямое вычисление ДПФ по выражению (12.2) требует выполнения весьма большого числа арифметических операций умножения и сложения, что затрудняет реализацию вычислений в реальном масштабе времени.

            Быстрым преобразованием Фурье (БПФ) называют набор алгоритмов, реализация которых приводит к существенному уменьшению вычислительной сложности ДПФ. Основная идея БПФ состоит в том, чтобы разбить исходный N-отсчетный сигнал x(n) на два более коротких сигнала, ДПФ которых могут быть скомбинированы таким образом, чтобы получить ДПФ исходного N-отсчетного сигнала.

            Так, если исходный N-отсчетный сигнал разбить на два N/2-отсчетных сигнала, то для вычисления ДПФ каждого из них потребуется около (N/2)2 комплексных умножений. Тогда для вычисления искомого N-отсчетного ДПФ потребуется порядка 2(N/2)2=N2/2 комплексных умножений , т.е. вдвое меньше по сравнению с прямым вычислением. Операцию разбиения можно повторить, вычисляя вместо (N/2)-отсчетного ДПФ два (N/4)-отсчетных ДПФ и сокращая тем сасым объем вычислений еще в два раза. Выигрыш в два раза является приблизительным, поскольку не учитывается, каким образом из ДПФ меньшего размера образуется искомое N-отсчетное ДПФ.

            Существует большое количество алгоритмов БПФ. Однако все они являются частными случаями единого алгоритма, базирующегося на задаче разбиения одного массива чисел на два. Тот факт, что это можно сделать более чем одним способом, определяет многообразие алгоритмов БПФ. Расмотрим два из них.

            Первый алгоритм называется алгоритмом БПФ с прореживанием по времени.

            Пусть задан N-отсчетный дискретный сигнал x(n). Примем, что N равно степени двойки. Если это не так, то всегда можно легко доплнить заданный сигнал нулевыми отсчетами до количества отсчетов, равного ближайшей степени двойки.

            Разобъем исходный сигнал x(n) на два N/2-отсчетных сигнала x1(n) и x2(n), составленных соответственно из четных и нечетных отсчетов исходного сигнала x(n)

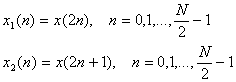                                                             (12.6).

N-точечное ДПФ сигнала x(n) можно записать как

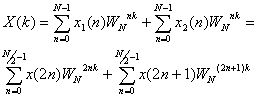                                            (12.7).

С учетом того, что

                                                             (12.8)

можно записать

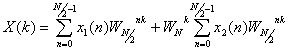                                               (12.9)

или

                                                                           (12.10),

где X1(k) и X2(k) – N/2-отсчетные ДПФ сигналов x1(n)  и x2(n) соответственно.

Таким образом N-точечное ДПФ X(k) может быть разложено на два N/2-точечных ДПФ, результаты которых объединяются согласно (12.10).

            Если бы N/2-точечные ДПФ вычислялись прямым способом, то для вычисления N-точечного ДПФ потребовалось бы (N2/2+N) комплексных умножений. При больших N (когда N2/2>>N) это позволяет сократить время вычислений на 50%.

            Поскольку X(k) определено при , а X1(k) и X2(k) определены при , необходимо доопределить формулу (12.10) для . Учитывая, что X1(k) и X2(k) – периодические функции с периодомN/2, можно записать

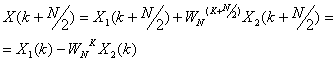                                    (12.11),

поскольку      .

            Поэтому окончательно для N-точечного ДПФ можно записать

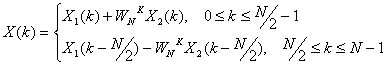                       (12.12).

            На рис.12.1 представлена последовательность операций при выполнении восьмиточечного ДПФ с использованием двух четырехточечных ДПФ.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


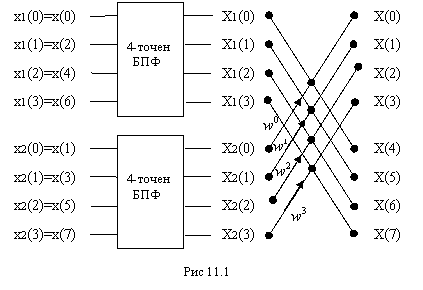
Сначала входной сигнал x(n) разбивается на два сигнала x1(n) и x2(n), составленных соответственно из четных и нечетных отсчетов x(n). После этого расчитывается ДПФ X1(k) и X2(k). Затем в соответствии с (12.12) получается X(k).

            Рассмотренная схема вычислений может быть использована и для расчета N/2-точечных ДПФ. В соответствии с этим каждый из сигналов x1(n) и x2(n) разбиваются на последовательности, состоящие из четных  и нечетных отсчетов родительских сигналов. Аналогично N/2-точечные ДПФ могут быть записаны как комбинации двух N/4-точечных ДПФ

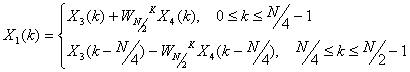                  (12.13).

С учетом того, что  можно записать

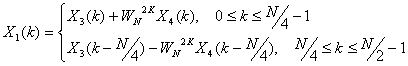                  (12.14).

            На рис.12.2 представлена последовательность операций при выполнении восьмиточечного ДПФ с использованием двух четырехточечных ДПФ и четырех двухточечных ДПФ.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


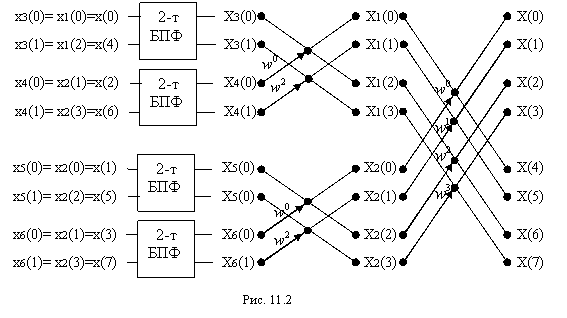
Таким образом, процесс уменьшения размера ДПФ может быть продолжен, пока не останутся только двухточечные ДПФ, которые могут быть рассчитаны без операции умножения

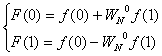                                           (12.15).

Поскольку , то окончательно получим

                                                                                      (12.16).

На рис.12.3 представлена порядок операций при последовательном вычислении восьмиточечного ДПФ в соответствии с описанным алгоритмом.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


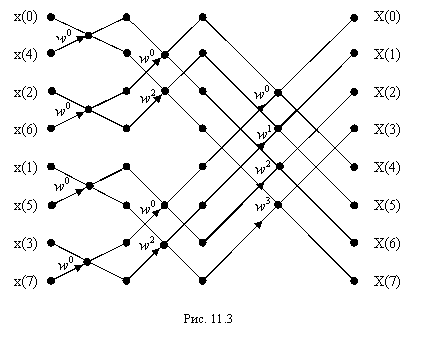
            Анализ рис.12.3 показывает, что на каждом этапе БПФ необходимо выполнить N/2 комплексных умножений. Поскольку общее количество этапов равно , то число комплексных умножений, необходимое для нахождения N-точечного ДПФ, приблизительно равно . Приблизительность оценки означает, что умножения на  в действительности сводятся просто к сложениям и вычитаниям комплексных чисел. Так на первом этапе алгоритма, представленного на рис.12.3, содержатся только сложения и вычитания комплексных чисел поскольку . Даже на втором этапе используются только сложения и вычитания комплексных чисел т.к. . Фактически вместо ожидаемых 12 () достаточно выполнить всего два нетривиальных умножения. Однако для больших значений N фактическое число нетривиальных умножений хорошо аппроксимируется выражением .

            Базовая операция алгоритма с прореживанием по времени (так называемая «бабочка») состоит в том, что два входных числа A и B объединяются для получения двух выходных чисел X и Y по правилу

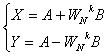                                                                                             (12.17).

На рис.12.4 изображен направленный граф базовой операции.

 

 

 

 

 

 

 

 


Каждый из этапов ДПФ содержит N/2 базовых операций. В случае когда  - нетривиальный множитель, для каждой базовой операции необходимо выполнить только одно умножение, поскольку величину  можно вычислить и запомнить. Таким образом структура базовых операций такова, что для выполнения БПФ N-отсчетного сигнала, отсчеты которого размещены в памяти, достаточно иметь лишь одну дополнительную ячейку памяти. Результаты всех промежуточных этапов БПФ можно размещать в те же ячейки памяти, где находились исходные данные. Алгоритм БПФ, в котором для размещения входной и выходной последовательности используется один и тот же массив памяти, называется алгоритмом с замещением.

            При реализации алгоритма необходима перестановка отсчетов входного сигнала, чтобы выходная последовательность имела естественный порядок расположения отсчетов, т.е. k=0,1,…,N-1. В приведенном примере для 8-точечного БПФ для этого требовался следующий порядок размещения отсчетов входного сигнала: x(0), x(4), x(2), x(6), x(1), x(5), x(3), x(7). Закономерность перестановки заключается в том, что отсчеты входного сигнала должны быть размещены в памяти в двоично-инверсном порядке. Это означает, что требуемый номер ячейки памяти для размещения очередного отсчета входного сигнала определяется обратной перестановкой двоичных разрядов в двоичном представлении номера отсчета. Для случая N=8 соответствие номеров отсчетов входного сигнала и их номеров ячеек памяти представлено в таблице 12.1.

Номер

Двоичное представление

Двоичная инверсия

Двоично-инверсный порядок

0

000

000

0

1

001

100

4

2

010

010

2

3

011

110

6

4

100

001

1

5

101

101

5

6

110

011

3

7

111

111

7

 

            На рис.12.5 показан алгоритм определения двоично-инверсного номера, предложенный Рейдером. Начиная с первого числа с прямым номером 0, этот алгоритм позволяет формировать последовательно все остальные двоично-инверсные номера.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


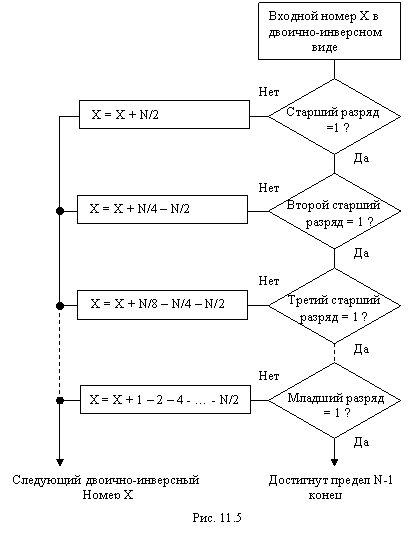
Половина из общего числа двоично-инверсных номеров формируются с использованием лишь двух операций, поскольку только в половине случаев старший разряд не равен единице. Аналогично четверть всех двоично-инверсных номеров формируется с использованием трех операций и т.д. таким образом, этот алгоритм является весьма эффективным.

            На всех этапах алгоритма БПФ используются коэффициенты . Существует несколько способов получения этих коэффициентов. Простейший способ – составление таблицы, к которой можно обращаться в процессе счета. В этом случае для определения коэффициентов не требуется дополнительных вычислений. Однако, для хранения таблицы коэффициентов необходима дополнительная память примерно из N ячеек.

            Второй способ заключается в непосредственном вычислении коэффициентов как

                                                           (12.18)

с использованием процедур вычисления синуса и косинуса. Этот способ связан с большими временными затратами.

            Третий способ основан на применении рекуррентной формулы

                                                                                             (12.19)

с начальным условием . При вычислении по описываемому алгоритму 16-точечного БПФ на первом этапе используются коэффициенты , на втором -  , на третьем - , на четвертом - . Поэтому, чтобы иметь возможность использовать формулу (12.19) на каждом из этапов, достаточно предварительно вычислить и запомнить коэффициенты .

            Рассмотрим еще один алгоритм БПФ, который называется алгоритм с прореживанием по частоте.

            Пусть снова имеем входной дискретный сигнал x(n), состоящий из N отсчетов, причем N равно степени двойки. Разобъем это сигнал на два N/2-отсчетных сигнала x1(n) и x2(n) так, что x1(n) состоит из первых N/2 отсчетов x(n), а x2(n) – из остальных N/2 отсчетов x(n), т.е.

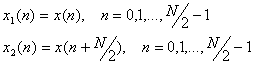                                                        (12.20).

При таком разбиении N-точечное ДПФ сигнала x(n) можно записать как

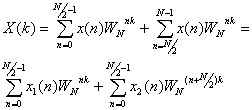                                                         (12.21).

Поскольку , то получим

                                                         (12.22).

Запишем выражения отдельно для четных и нечетных отсчетов ДПФ.

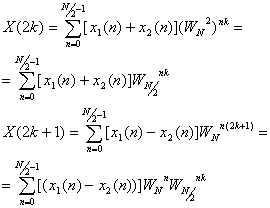                                                     (12.23).

Из выражения (12.23) видно, что N-точечное ДПФ можно получить как сумму двух N/2-точечных ДПФ N/2-отсчетных сигналов: сигнала  и сигнала  .

            Аналогично предыдущему алгоритму, описанную процедуру можно применить повторно и представить каждое из N/2-точечных ДПФ в виде комбинации двух N/4-точечных ДПФ и т.д. На рис.12.6 представлен пример 8-точечного БПФ, реализованного по этому алгоритму.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


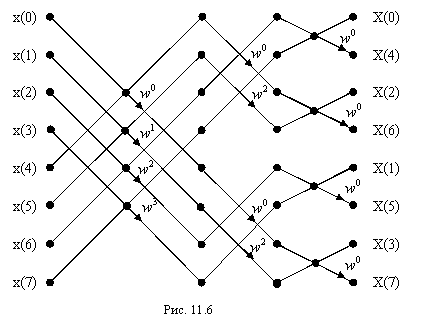
            Базовая операция этого алгоритма описывается выражением

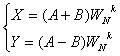                                                                                          (12.24).

            Сравнение двух описанных алгоритмов позволяет выявить два очевидных различия между ними. Во-первых, при прореживании по времени порядок следования входных отсчетов двоично-инверсный, а выходных – прямой. При прореживании по частоте – наоборот. Однако это отличие кажущееся, поскольку в обоих алгоритмах порядок следования входных отсчетов можно сделать прямым. Тогда порядок следования выходных отсчетов будет двоично-инверсным. И наоборот.

            Второе отличие заключается в несколько ином выполеннии базовой операции. При прореживании по частоте комплексное умножение выполняется после сложения-вычитания.

            В обоих алгоритмах для вычисления N-точечного ДПФ требуется около  операций комплексного умножения. Вычисления по обоим алгоритмам могут быть произведены с замещением. В обоих случаях должно быть предусмотрено выполнение двоичной инверсии.

            Обратное ДПФ N-точечной последовательности X(k), k=0,1,…,N-1 определяется как

                                                                                (12.25).

Взяв выражение, комплексно-сопряженное с (12.25) и умножив его на N получим

                                                                                (12.26).

Однако, правая часть (12.26) представляет собой прямое ДПФ последовательности X*(k) и может быть вычислена с использованием одного из вышеописанных алгоритмов БПФ. Искомую последовательность x(n) можно получить, взяв комплексно-сопряженное с (12.26) выражение и разделив его на N

                                                                            (12.27).

Таким образом, алгоритмы БПФ обеспечивают вычисление и прямого и обратного ДПФ.

            Алгоритмы БПФ могут быть использованы для вычисления реакции цифрового фильтра.

            Если на вход фильтра N-го порядка с импульсной характеристикой h(n) подан входной сигнал x(n), то реакция фильтра может быть вычислена по правилу свертки

                                                                                (12.28).

            Применение алгоритмов БПФ позволяет выполнить эффективное вычисление выходного сигнала y(n) цифрового фильтра. С этой целью следует определить ДПФ H(k) и X(k) в N+M-1 точках для последовательностей h(n) и x(n), затем определить ДПФ Y(k)=X(k)H(k) выходного сигнала y(n). Вычисление y(n) по правилу обратного ДПФ выполняется также с помощью алгоритмов БПФ. Однако, если длина M последовательности x(n) велика, то реализация такого алгоритма вычисления y(n) связана со значительной временной задержкой, необходимой для накопления всех M выборок x(n). С целью уменьшения этой задержки можно входной сигнал x(n) разбить на отрезки xi(n) каждый длиной L и обрабатывать каждый из нихнезависимо от других. Представим

                                                 (12.29).

Тогда можно (12.28) записать в виде

                                                         (12.30),

где частная свертка yi(n) определяется как

                                                                              (12.31).

Таким образом можно начинать расчет с помощью алгоритмов БПФ частных сверток и формировать выходной сигнал фильтра y(n) путем соответствующего суммирования элементов частных сверток.