Лекция №

«Цифровые фильтры с бесконечной импульсной характеристикой»

 

           

            Передаточная функция физически реализуемого цифрового фильтра с бесконечной импульсной характеристикой (БИХ-фильтра) может быть представлена в виде

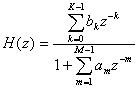                                                                                     (11.1).

Вид дискретной передаточной функции БИХ-фильтра аналогичен виду непрерывной передаточной функции аналоговых фильтров. Поэтому можно использовать структуры цифровых БИХ-фильтров для для получения частотных характеристик, соответствующих классическим видам аппроксимации (фильтры Баттерворта, Чебышева, Бесселя и пр.). Однако, реализовать цифровой фильтр с частотной характеристикой, точно совпадающей с частотной характеристикой аналогового фильтра невозможно. Причиной этого является тот факт, что, в отличие от аналогового фильтра в диапазоне частот цифровой фильтр обладает периодической частотной характеристикой с периодом, равным частоте дискретизации fs. Однако используемая полоса частот у цифровых фильтров ограничивается диапазоном . Поэтому поставленную задачу можно видоизменить таким образом, чтобы частотная характеристика цифрового фильтра совпадала с требуемой частотной характеристикой аналогового фильтра лишь в диапазоне частот .

Для этого нужно модифицировать передаточную функцию аналогового фильтра посредством преобразования оси частот таким образом, чтобы диапазон отображался в диапазон  и на высоких частотах периодически повторялся. Для этого введем

                                                                                  (11.2).

При , как и требуется, . При  имеем . Искажение частотной оси, вносимое таким преобразованием, тем меньше, чем больше частота дискретизации по сравнению с интересующим нас диапазоном частот.

Свойства цифрового фильтра на определенной частоте определяется отношением этой частоты к частоте дискретизации. Поэтому введем нормированные частот

                                                                (11.3),

где   -  частота среза фильтра.

При этом из (11.2) получим

                                                                                   (11.4).

В качестве примера преобразования частотной оси на рис.11.1. приведена АЧХ аналогового фильтра и соответствующая АЧХ преобразованного фильтра.

 

 

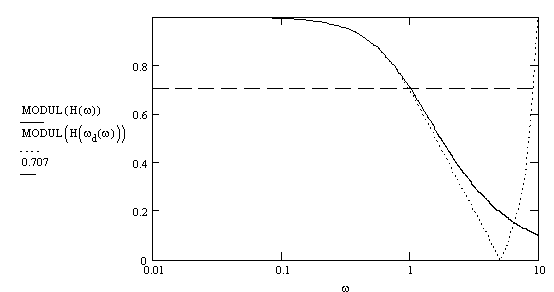
                                                Рис.11.1

 

Видно, что преобразованная характеристика приблизительно совпадает с исходной на начальном участке оси частот, а в дальнейшем представляет из себя периодическую функцию частоты, что соответствует цифровому фильтру. Из рисунка видно, что произошел сдвиг частоты среза фильтра.

Для того, чтобы в процессе преобразования не смещалась частота среза фильтра необходимо, чтобы при  выполнялось равенство . Для этого необходимо модифицировать формулу преобразования

                                                                                  (11.5),

где                                                                                               (11.6).

Преобразованная частотная характеристика представлена на рис.11.2.

 

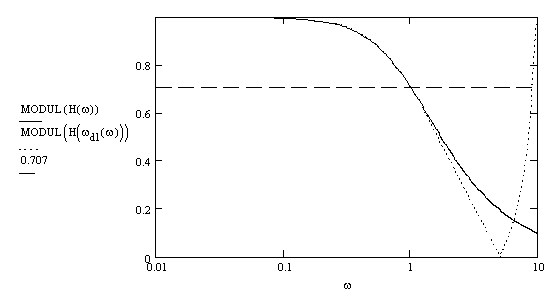
                                                                                    Рис.11.2

 

Очевидно, что полученная характеристика подобна характеристике аналогового фильтра в диапазоне частот .

            Благодаря описанным операциям преобразования преобразованная частотная характеристика имеет вид, позволяющий реализовать ее с помощью цифрового фильтра. Для расчета передаточной функции цифрового фильтра H(z) необходимо иметь уравнение преобразования переменной p в переменную z.  Изначально аналоговые фильтры задаются в нормированном виде, т.е. с частотой среза 1 рад/сек. Поэтому введем нормированную комплексную переменную p

                                                                       (11.7),

где                                                                                                 (11.8).

При подстановке в выражение (11.7) выражения (11.5) получим

                                                                          (11.9).

Из формулы Эйлера

                                                                                   (11.10)

вытекают следующие соотношения

                         (11.11).

Используя эти соотношения в (11.9) получим

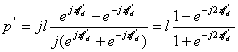                                                            (11.12).

С учетом того, что

 

                                                          (11.13),

 

 получим

                                                                          (11.14).

Однако . Поэтому

                                                                                     (11.15),

 

при                                                                                              (11.16).

 

Это соотношение называется билинейным преобразованием.

            Таким образом, аналоговый фильтр можно преобразовать в цифровой следующим образом. В выражение для передаточной функции H(p) нормированного аналогового фильтра вместо переменой p подставляется переменная  и получаем передаточную функцию H(z) цифрового фильтра с аналогичной частотной характеристикой в диапазоне частот .

            Фазо-частотная характеристика при билинейном преобразовании изменяется сильнее. По этой причине не имеет смысла применять билинейное преобразование к фильтрам Бесселя, поскольку линейность ФЧХ в этом случае нарушается.

            При построении цифровых фильтров, как и для аналоговых фильтров, наиболее просто соединять блоки первого и второго порядка. Поэтому произведем пересчет коэффициентов передаточной функции аналогового фильтра H(p) в коэффициенты передаточной функции цифрового фильтра H(z) для звеньев первого и второго порядка. Используя билинейное преобразование, из выражения для аналоговой передаточной функции

                                                                               (11.17)

найдем дискретную передаточную функцию

                                                                                (11.18).

Для фильтра первого порядка () будем иметь

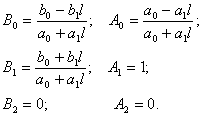                                                                      (11.19).

Для фильтра второго порядка () будем иметь

                                                (11.20).

            Порядок действий при определении передаточной функции H(z) цифрового ФНЧ по заданным требованиям к максимально допустимой неравномерности АЧХ в полосе пропускания Ap, минимально допустимому затуханию в полосе задерживания Aa, а также граничным нормированным частотам полосы пропускания wp и полосы задерживания wa должен быть следующим.

            Вначале определяются нормированные частоты полосы пропускания и полосы задерживания аналогичного аналогового фильтра с помощью нелинейного соотношения (11.7). После этого, одним из способов синтеза аналоговых фильтров определяется аналоговая передаточная функция H(p’) фильтра-прототипа, удовлетворяющего заданным требованиям неравномерности АЧХ в полосе пропускания и затуханию в полосе задерживания.

В заключение в определенной передаточной функции аналогового фильтра делается замена переменной p в соответствии с (11.15).

            Существует более общее преобразование, разработанное Констандинидисом и позволяющее преобразовывать аналоговый ФНЧ в избирательный БИХ-фильтр любого типа (ФНЧ, ФВЧ, ПФ, ЗФ). Не рассматривая вывода соответствующих формул приведем их в таблице 11.1.

 

 

 

 

Цифровой фильтр

Граничные цифровые частоты

Формула замены

Параметр

Связь аналоговых частот с цифровыми частотами

Граничные аналоговые частоты

Нижних частот

Верхних частот

Полосовой

Режекторный

 

 

 

 

Для обеспечения требуемого качества работы фильтра необходимо не только нейти требуемую передаточную функцию, но и оценить достаточную разрядность входного и выходного сигнала, а также коэффициентов фильтра.

Количество разрядов для представления коэффициентов фильтра определяется с помощью итерационной процедуры из условия удовлетворения передаточной функции фильтра с квантованными коэффициентами, заданных требований по приближению к эталонной передаточной функции с точными значениями коэффициентов.

            Абсолютные величины отсчетов входных сигналов фильтра обычно нормированы так, что

                                                                                                         (11.21).

            Разрядность входного сигнала  и разрядность сумматоров цифрового фильтра определяются на основе оценок составляющих шума квантования выходного сигнала, обусловленных квантованием входного сигнала (входного шума) и квантованием выходных кодов сумматоров фильтра (собственного шума), а также оценок диапазона изменения сигналов в фильтре. При этом допустимая величина мощности выходного шума фильтра распеределяется в определенной пропорции на составляющие выходного шума, обусловленные входными и собственными шумами фильтра

                                                                                      (11.22),

где  и - составляющие выходного шума фильтра, обусловленные соответственно входным шумом и собственными шумами фильтра, - максимально допустимый уровень мощности выходного шума фильтра, K – коэффициент (K=0.8 – 0.9).

            Как извесно, дисперсия шума округления входного сигнала  связана с разрядностью входного сигнала как

                                                                                                   (11.23).

            В тоже время, дисперсия выходного шума определяется как

                                                           (11.24),

т.е. зависит от дисперсии шума округления входного сигнала и значений отсчетов импульсной характеристики фильтра. Отсюда можно найти требуемое количество разрядов входного сигнала как

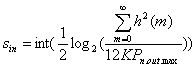                                                                       (11.25).

Количество разрядов для представления дробной части выходного кода сумматоров зависит от структуры фильтра и определяется по формуле

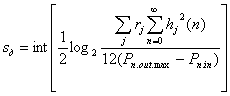                                                               (11.26),

где - число умножителей, подключенных к j-му сумматору, hj(n) – импульсная характеристика части фильтра от выхода j-го сумматора до выхода фильтра.

            Количество разрядов  для представления целой части переменных фильтра определяется на основне оценки диапазона изменения сигналов в фильтре. Как известно, диапазон изменения сигнала на выходе j-го сумматора фильтра определяется как

                                                                                                (11.27),

где hj(n) – импульсная характеристика части фильтра от входа до выхода j-го сумматора. Поэтому величину можно определить как

                                                                           (11.28),

где  - коэффициент l-го умножителя, подключенного к выходу j-го сумматора.

            Расчет по формуле (11.27) гарантирует отсутствие переполнений при нулевых начальных условиях.

            Общая разрядность s, ячеек памяти фильтра определяется как

                                                                                                      (11.29).