Лекция №10
«Цифровые фильтры с конечной импульсной характеристикой»
Передаточная функция физически реализуемого цифрового фильтра с конечной импульсной характеристикой (КИХ-фильтра) может быть представлена в виде
![]() (10.1).
(10.1).
При
замене в выражении (10.1) ![]() получим частотную характеристику
КИХ-фильтра в виде
получим частотную характеристику
КИХ-фильтра в виде
![]() (10.2),
(10.2),
где
![]() - амплитудно-частотная
характеристика (АЧХ) фильтра,
- амплитудно-частотная
характеристика (АЧХ) фильтра,
![]() - фазо-частотная
характеристика (ФЧХ) фильтра.
- фазо-частотная
характеристика (ФЧХ) фильтра.
Фазовая задержка фильтра определяется как
![]() (10.3).
(10.3).
Групповая задержка фильтра определяется как
![]() (10.4).
(10.4).
Отличительной особенностью КИХ-фильтров является возможность реализации у них постоянных фазовой и групповой задержек, т.е. линейной ФЧХ
![]() (10.5),
(10.5),
где a - константа. При соблюдении этого условия сигнал, проходящий через фильтр, не искажает своей формы.
Для вывода условий, обеспечивающих линейную ФЧХ запишем частотную характеристику КИХ-фильтра с учетом (10.5)
![]() (10.6).
(10.6).
Приравнивая действительные и мнимые части этого равенства, получим
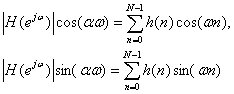 (10.7).
(10.7).
Разделив второе уравнение на первое, получим
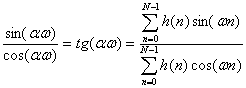 (10.8).
(10.8).
Окончательно можно записать
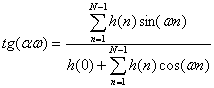 (10.9).
(10.9).
Это уравнение имеет два решения. Первое при a=0 соответствует уравнению
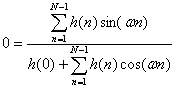 (10.10).
(10.10).
Это уравнение имеет единственное решение, соответствующее произвольному h(0) (sin(0)=0), и h(n)=0 при n>0. Это решение соответствует фильтру, импульсная характеристика которого имеет единственный ненулевой отсчет в начальный момент времени. Такой фильтр на представляет практического интереса.
Другое
решение найдем для ![]() .
При этом перекрестно перемножив числители и знаменатели в (10.8) получим
.
При этом перекрестно перемножив числители и знаменатели в (10.8) получим
![]() (10.11).
(10.11).
Отсюда имеем
![]() (10.12).
(10.12).
Поскольку это уравнение имеет вид ряда Фурье, то его решение, если оно существует, является единственным.
Легко заметить, что решение этого уравнения должно удовлетворять условиям
![]() (10.13),
(10.13),
![]() (10.14).
(10.14).
Из
условия (10.13) следует, что для каждого порядка фильтра N
существует только одна фазовая задержка a, при которой может
достигаться строгая линейность ФЧХ. Из условия (10.14) следует, что импульсная
характеристика фильтра должна быть симметричной относительно точки ![]() для нечетного N, и
относительно средней точки интервала
для нечетного N, и
относительно средней точки интервала ![]() (рис.10.1).
(рис.10.1).
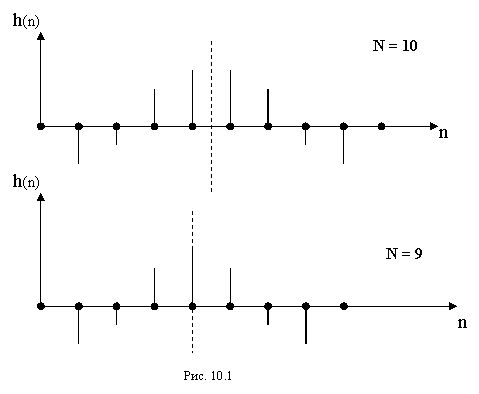 |
Частотную характеристику такого фильтра (для нечетного N) можно записать в виде
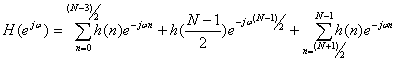 (10.15).
(10.15).
Делая во второй сумме замену m=N-1-n, получим
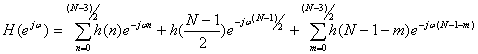 (10.16).
(10.16).
Поскольку h(n)=h(N-1-n), то две суммы можно объединить
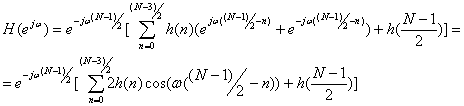 (10.17).
(10.17).
Подставив
![]() ,
получим
,
получим
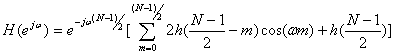 (10.18).
(10.18).
Если обозначить
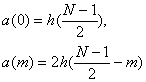 (10.19),
(10.19),
то окончательно можно записать
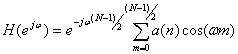 (10.20).
(10.20).
Таким образом, для фильтра с линейной ФЧХ имеем
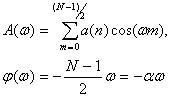 (10.21).
(10.21).
Для случая четного N аналогично будем иметь
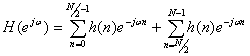 (10.22).
(10.22).
Делая
замену во второй сумме ![]() , получим
, получим
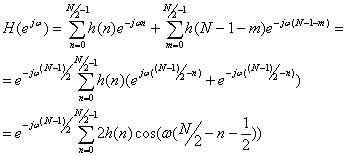 (10.23).
(10.23).
Делая
замену ![]() ,
получим
,
получим
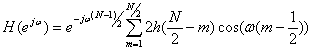 (10.24).
(10.24).
Обозначив
![]() (10.25),
(10.25),
будем окончательно иметь
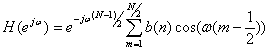 (10.26).
(10.26).
Таким образом, для КИХ-фильтра с линейной ФЧХ и четным порядком N можно записать
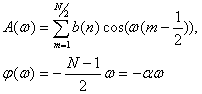 (10.27).
(10.27).
В дальнейшем, для простоты будем рассматривать только фильтры с нечетным порядком.
При синтезе передаточной функции фильтра исходными параметрами, как правило, являются требования к частотной характеристике. Существует много методик синтеза КИХ-фильтров. Рассмотрим некоторые из них.
Поскольку частотная характеристика любого цифрового фильтра является периодической функцией частоты, то ее можно представить в виде ряда Фурье
![]() (10.28),
(10.28),
где коэффициенты ряда Фурье равны
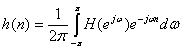 (10.29).
(10.29).
Видно, что коэффициенты ряда Фурье h(n) совпадают с коэффициентами импульсной характеристики фильтра. Поэтому, если известно аналитическое описание требуемой частотной характеристики фильтра, то по нему можно легко определить коэффициенты импульсной характеристики, а по ним – передаточную функцию фильтра. Однако на практике это не реализуемо, поскольку импульсная характеристика такого фильтра имеет бесконечную длину. Кроме того, такой фильтр физически не реализуем поскольку импульсная характеристика начинается в -¥, и никакая конечная задержка не сделает это фильтр физически реализуемым.
Одним
из возможных методов получения КИХ-фильтра, аппроксимирующего заданную
частотную характеристику заключается в усечении бесконечного ряда Фурье и
импульсной характеристики фильтра, полагая что h(n)=0
при ![]() . Тогда
. Тогда
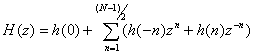 (10.30).
(10.30).
Физическая
реализуемость передаточной функции H(z) может быть
достигнута путем умножения H(z) на ![]() .
.
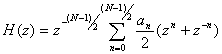 (10.31),
(10.31),
где
![]() (10.32).
(10.32).
При
такой модификации передаточной функции амплитудная характеристика фильтра не
изменяется, а групповая задержка увеличивается на постоянную величину ![]() .
.
В качестве примера расчитаем КИХ-фильтр низких частот с частотной характеристикой вида
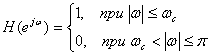 (10.33).
(10.33).
В соответствии с (10.29) коэффициенты импульсной характеристики фильтра описываются выражением
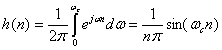 (10.34).
(10.34).
Теперь из (10.31) можно получить выражение для передаточной функции
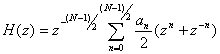 (10.35),
(10.35),
где
![]() (10.36).
(10.36).
Амплитудные характеристики рассчитанного фильтра для различных N представлены на рис.10.2.
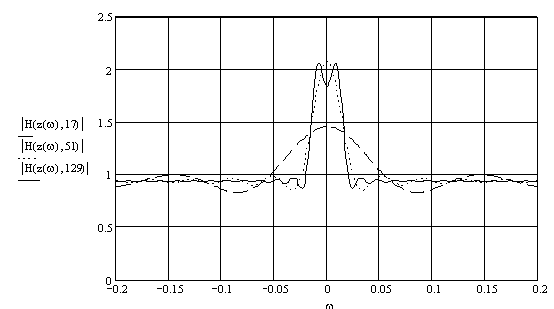
Рис.10.2
Пульсации в полосах пропускания и задерживания происходят
вследствие медленной сходимости ряда Фурье, которая, в свою очередь,
обусловлена наличием разрыва функции ![]() на частоте среза полосы пропускания. Эти
пульсации известны как пульсации Гиббса.
на частоте среза полосы пропускания. Эти
пульсации известны как пульсации Гиббса.
Из рис.10.2 видно, что с увеличением N частота пульсаций растет, а амплитуда уменьшается как на нижних, так и на верхних частотах. Однако амплитуда последней пульсации в полосе пропускания и первой пульсации в полосе задерживания остаются практически неизменными. На практике такие эффекты часто нежелательны, что требует отыскания путей снижения пульсаций Гиббса.
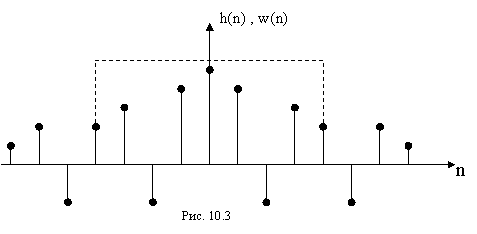
Усеченную импульсную характеристику h(n) можно представить в виде произведения требуемой бесконечной импульсной характеристики и некоторой функции окна w(n) длины n (рис.10.3).
![]() (10.37).
(10.37).
 |
В рассмотренном случае простого усечения ряда Фурье используется прямоугольное окно
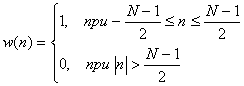 (10.38).
(10.38).
В этом случае частотную характеристику фильтра можно представить в виде комплексной свертки
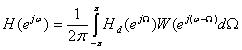 (10.39).
(10.39).
Это
значит, что ![]() будет
«размытой» версией требуемой характеристики
будет
«размытой» версией требуемой характеристики ![]() .
.
Задача сводится к отысканию функций окон, позволяющих уменьшить пульсации Гиббса при той же избирательности фильтра. Для этого необходимо вначале изучить свойства функции окна на примере прямоугольного окна.
Спектр функции прямоугольного окна можно записать как
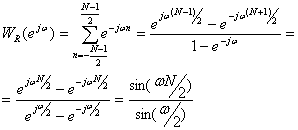 (10.40).
(10.40).
Спектр функции прямоугольного окна представлен на рис.10.4.
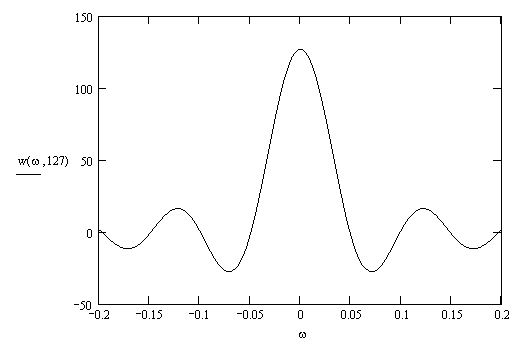
Рис.10.4
Поскольку
![]() при
при ![]() , то ширина главного
лепестка спектра оказывается равной
, то ширина главного
лепестка спектра оказывается равной ![]() .
.
Наличие боковых лепестков в спектре функции окна приводит к увеличению пульсаций Гиббса в АЧХ фильтра. Для получения малых пульсаций в полосе пропускания и большого затухания в полосе задерживания необходимо, чтобы площадь, ограниченная боковыми лепестками, составляла малую долю от площади, ограниченной главным лепестком.
В свою очередь, ширина главного лепестка определяет ширину переходной зоны результирующего фильтра. Для высокой избирательности фильтра ширина главного лепестка должна быть по возможности малой. Как видно из вышеизложенного, ширина главного лепестка уменьшается с увеличением порядка фильтра.
Таким образом, свойства подходящих функций окна можно сформулировать следующим образом:
- функция окна должна быть ограничена во времени;
- спектр функции окна должен наилучшим образом аппроксимировать функцию, ограниченную по частоте, т.е. иметь минимум энергии за пределами основного лепестка;
- ширина основного лепестка спектра функции окна должна по возможности малой.
Наиболее часто используют следующие функции окон:
1. Прямоугольное окно. Рассмотрено выше.
2. Окно Хэмминга (Hamming).
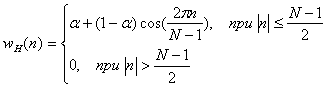 (10.41),
(10.41),
где ![]() .
.
При ![]() это окно называется окном Хэнна (hanning).
это окно называется окном Хэнна (hanning).
3. Окно Блэкмана (Blackman).
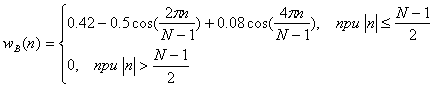 (10.42).
(10.42).
4. Окно Бартлета (Bartlett).
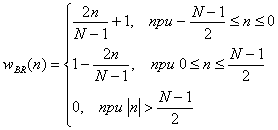 (10.43).
(10.43).
Показатели фильтров, построенных с применением указанных функций окон, сведены в таблицу 10.1.
|
Окно |
Ширина главного лепестка |
Коэффициент пульсаций, % |
||
N=11 |
N=21 |
N=31 |
||
|
Прямоугольное |
|
22.34 |
21.89 |
21.80 |
|
Хэннинга |
|
2.62 |
2.67 |
2.67 |
|
Хэмминга |
|
1.47 |
0.93 |
0.82 |
|
Блэкмана |
|
0.08 |
0.12 |
0.12 |
Коэффициент пульсации определяется как отношение максимальной амплитуды бокового лепестка к амплитуде главного лепестка в спектре функции окна.
Для выбора требуемого порядка фильтра и наиболее подходящей функции окна при расчете реальных фильтров можно использовать данные таблицы 10.2.
|
Окно |
Ширина переходной полосы |
Неравномерность в полосе пропускания (дБ) |
Затухание в полосе заграждения (дБ) |
|
Прямоугольное |
|
0.7416 |
21 |
|
Хэннинга |
|
0.0546 |
44 |
|
Хэмминга |
|
0.0194 |
53 |
|
Блэкмана |
|
0.0017 |
75 |
Как видно из таблицы 10.1, существует определенная зависимость между коэффициентом пульсаций и шириной главного лепестка в спектре функции окна. Чем меньше коэффициент пульсаций, тем больше ширина главного лепестка, а значит и переходной зоны в АЧХ фильтра. Для обеспечения малой пульсации в полосе пропускания приходится выбирать окно с подходящим коэффициентом пульсаций, а требуемую ширину переходной зоны обеспечивать повышенным порядком фильтра N.
Эту проблему можно решить с помощью окна, предложенного Кайзером (Kaiser). Функция окна Кайзера имеет вид
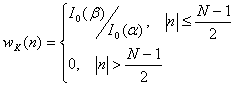 (10.44),
(10.44),
где a - независимый параметр, ![]() , I0
– функция Бесселя первого рода нулевого порядка, определяемая выражением
, I0
– функция Бесселя первого рода нулевого порядка, определяемая выражением
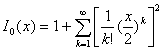 (10.45).
(10.45).
Привлекательным свойством окна Кайзера является возможность плавного изменения коэффициента пульсаций от малых значений до больших, при изменении только одного параметра a. При этом как и для других функций окон ширина главного лепестка может регулироваться порядком фильтра N.
Основными параметрами, задаваемыми при разработке реального фильтра являютя:
- полоса пропускания - wp;
- полоса заграждения - wa;
- максимально допустимая пульсация в полосе пропускания – Ap;
- минимальное затухание в полосе задерживания – Aa;
- частота дискретизации - ws.
Эти параметры иллюстрируются на рис.10.5. При этом максимальная пульсация в полосе пропускания определяется как
![]() (10.46),
(10.46),
а минимальное затухание в полосе задерживания как
![]() (10.47).
(10.47).
Сравнительно простая процедура расчета фильтра с окном Кайзера включает в себя следующие этапы:
1. Определяется импульсная характеристика фильтра h(n) при условии, частотная характеристика является идеальной
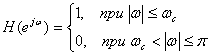 (10.48),
(10.48),
где ![]() (10.49).
(10.49).
2. Выбирается параметр d как
![]() (10.50),
(10.50),
где 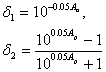 (10.51).
(10.51).
3. Вычисляется истинное значение Aa и Ap по формулам (10.46), (10.47).
4. Выбирается параметр a как
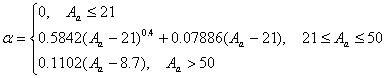 (10.52).
(10.52).
5. Выбирается параметр D как
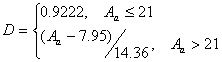 (10.53).
(10.53).
6. Выбирается наименьшее нечетное значение порядка фильтра из условия
![]() (10.54),
(10.54),
где ws – частота дискретизации.
7. Записывается выражение для функции окна Кайзера с учетом найденных параметров a и N.
8. Записывается выражение для передаточной функцией фильтра в виде
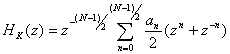 (10.55),
(10.55),
где ![]() (10.56).
(10.56).
Формулы для расчета импульсных характеристик фильтров различных типов представлены в таблице 10.3.
|
Тип фильтра |
|
|
|
Фильтр низких частот |
|
|
|
Фильтр высоких частот |
|
|
|
Полосовой фильтр |
|
|
|
Заградительный фильтр |
|
|
Здесь ![]() - нормированные частоты краев полос
пропускания или заграждения.
- нормированные частоты краев полос
пропускания или заграждения.
Для обеспечения требуемого качества работы фильтра необходимо не только нейти требуемую передаточную функцию, но и оценить достаточную разрядность входного и выходного сигнала, а также коэффициентов фильтра.
Поскольку АЧХ фильтра нормируются так, чтобы при всех значениях частоты модуль передаточной функции фильтра не превышал единицы, то из теоремы Парсеваля
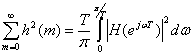 (10.57)
(10.57)
следует, что
![]() (10.58),
(10.58),
т.е.
![]() (10.59).
(10.59).
Поскольку отсчеты импульсной характеристики фильтра являются коэффициентами его передаточной функции, то условие (10.59) означает, что коды всех коэффициентов фильтра содержат лишь дробную часть и знаковый разряд и не содержат целой части.
Количество разрядов дробной части коэффициентов фильтра определяется из условия удовлетворения передаточной функции фильтра с квантованными коэффициентами, заданных требований по приближению к эталонной передаточной функции с точными значениями коэффициентов.
Абсолютные величины отсчетов входных сигналов фильтра обычно нормированы так, что
![]() (10.60).
(10.60).
Если анализ проводится для КИХ-фильтра с линейной ФЧХ, то алгоритм вычисления его выходного сигнала может быть следующим
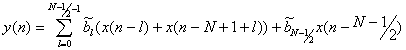 (10.61),
(10.61),
где ![]() - округленные до sk коэффициенты фильтра.
- округленные до sk коэффициенты фильтра.
Этому алгоритму соответствует структурная схема фильтра, представленная на рис.10.5.
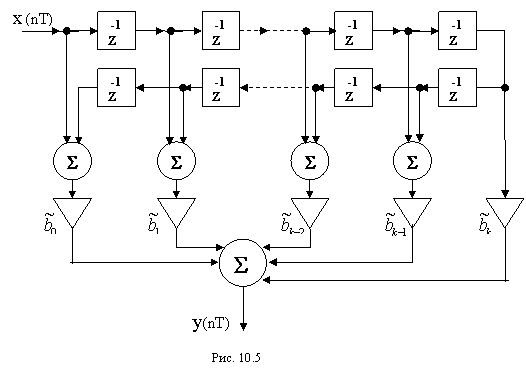 |
Существуют два способа реализации этого алгоритма. В первом случае все операции умножения выполняются точно и округление произведений отсутствует. В этом случае разрядность произведений равна sin+sk, где sin – разрядность входного сигнала, а sk – разрядность коэффициентов фильтра. В этом случае структурная схема фильтра, представленная на рис.10.5 точно соответствует реальному фильтру.
При втором способе реализации алгоритма (10.61) каждый результат операции умножения округляется, т.е. произведения вычисляются с некоторой погрешностью. В этом случае необходимо изменить алгоритм (10.61) так, чтобы учесть погрешность вносимую, округлением произведений
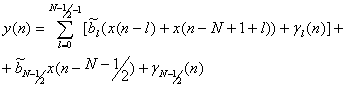 (10.62),
(10.62),
где ![]() - величины погрешностей
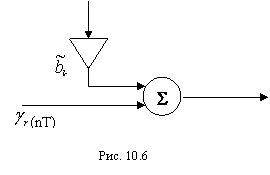
вычисления соответствующих произведений. В этом случае на структурной схеме
фильтра каждый умножитель должен быть дополнен сумматором точного произведения
и погрешности (рис.10.6).
- величины погрешностей
вычисления соответствующих произведений. В этом случае на структурной схеме
фильтра каждый умножитель должен быть дополнен сумматором точного произведения
и погрешности (рис.10.6).
 |
Из (10.60) и (10.61) следует, что
![]() (10.63),
(10.63),
откуда следует, что количество разрядов для целой части кода выходного сигнала фильтра sц может быть определено как
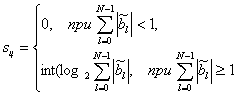 (10.64).
(10.64).
пусть задана
величина допустимой дисперсии шума на выходе фильтра ![]() . Как извесно, дисперсия шума
округления входного сигнала
. Как извесно, дисперсия шума
округления входного сигнала ![]() связана с разрядностью входного сигнала
как
связана с разрядностью входного сигнала
как
![]() (10.65).
(10.65).
Если значения отсчетов выходного сигнала фильтра вычисляются по первому способу (с точными значениями произведений), то дисперсия выходного шума определяется как
![]() (10.66),
(10.66),
т.е. зависит от дисперсии шума округления входного сигнала и значений коэффициентов фильтра. Отсюда можно найти требуемое количество разрядов входного сигнала как
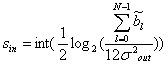 (10.67).
(10.67).
По известным значениям sin и sk можно определить количество разрядов, необходимое для дробной части кода выходного сигнала как
![]() (10.68).
(10.68).
Если значения отсчетов выходного сигнала вычисляются по второму способу, когда каждое произведение округляется до sд разрядов, то дисперсию шума округления, создаваемого каждым из умножителей можно выразить через разрядность произведения как
![]() (10.69).
(10.69).
Из (10.62) следует, что в этом случае дисперсия выходного шума фильтра определяется как
![]() (10.70).
(10.70).
При этом мощность собственных шумов фильтра должна быть мала по сравнению с мощностью шума округления входного сигнала
![]() ,
,
т.е. ![]() (10.71),
(10.71),
где K<<1 (можно например принять K=0.1). Из (10.69)-(10.71) следуют формулы для определения требуемой разрядности входного сигнала и количества разрядов для дробной части выходного сигнала
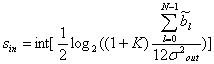 (10.72),
(10.72),
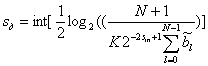 (10.73).
(10.73).
Требуемое значение дисперсии выходного шума фильтра, которая является исходным параметром для вычисления всех разрядностей, можно определить исходя из заданных значений динамического диапазона входного сигнала фильтра DRin и отношения сигнал-шум на выходе фильтра SNRout. Значение динамического диапазона входного сигнала в децибелах определяется как
![]() (10.74),
(10.74),
где Amax и Amin – максимальная и минимальная амплитуды входного сигнала фильтра.
Отношение сигнал-шум на выходе фильтра, выраженное в децибелах, определяется как
![]() (10.75),
(10.75),
где ![]() (10.76)
(10.76)
определяет среднеквадратическое значение мощности выходного синусоидального сигнала фильтра с амплитудой Amin, а
![]() (10.77)
(10.77)
определяет мощность шума на выходе фильтра. Из (10.75) и (10.76) при Amax=1 получаем выражение для дисперсии выходного шума фильтра
![]() (10.78).
(10.78).
Это значение дисперсии выходного шума фильтра может быть использовано для вычисления разрядностей входного и выходного сигналов фильтра.