Лекция № 1

 

«Аналоговые, дискретные и цифровые сигналы.»

 

            Двумя самыми фундаментальными понятиями в данном курсе являются понятия сигнала и системы.

Под сигналом понимается физический процесс (например, изменяющееся во времени напряжение), отображающий некоторую информацию или сообщение. Математически сигнал описывается функцией определенного типа.

            Одномерные сигналы описываются вещественной или комплексной функцией , определенной на интервале вещественной оси (обычно – оси времени) . Примером одномерного сигнала может служить электрический ток в проводе микрофона, несущий информацию о воспринимаемом звуке.

            Сигнал x(t) называется ограниченным если существует положительное число A, такое, что для любого t .

            Энергией сигнала x(t) называется величина

                                                ,                                                (1.1)

Если , то говорят, что сигнал x(t) имеет ограниченную энергию. Сигналы с ограниченной энергией обладают свойством

                                                .

 Если сигнал имеет ограниченную энергию, то он ограничен.

            Мощностью сигнала x(t) называется величина

                                                ,                                   (1.2)

Если , то говорят, что сигнал x(t) имеет ограниченную мощность. Сигналы с ограниченной мощностью  могут принимать ненулевые значения сколь угодно долго.

            В реальной природе сигналов с неограниченной энергией и мощностью не существует. Большинство сигналов, существующих в реальной природе являются аналоговыми.

Аналоговые сигналы описываются непрерывной (или кусочно-непрерывной) функцией , причем сама функция и аргумент t могут принимать любые значения на некоторых интервалах . На рис. 1.1а представлен пример аналогового сигнала, изменяющегося во времени по закону , где . Другой пример аналогового сигнала, показанный на рис 1.1б, изменяется во времени по закону .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


Важным примером аналогового сигнала является сигнал, описываемый т.н. «единичной функцией», которая описывается выражением

                                                                        (1.3),

где                               .

График единичной функции представлен на рис.1.2.

 

 

 

 

 

 

 

 

 

 

 

 


Функцию 1(t) можно рассматривать как предел семейства непрерывных функций 1(a,t) при изменении параметра этого семейства a.

                                                                   (1.4).

Семейство графиков 1(a,t) при различных значениях a представлено на рис.1.3.

 

 

 

 

 

 

 

 

 

 

 

 

 


В этом случае функцию 1(t) можно записать как

                                                                                             (1.5).

Обозначим производную от 1(a,t) как d(a,t).

                                                                    (1.6).

Семейство графиков d(a,t) представлено на рис.1.4.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


Площадь под кривой d(a,t) не зависит от a и всегда равна 1. Действительно

                     (1.7).

Функция

                                                                                           (1.8)

называется импульсной функцией Дирака или d-функцией. Значения d-функции равны нулю во всех точках, кроме t=0. При t=0 d-функция равна бесконечности, но так, что площадь под кривой d-функции равна 1. На рис.1.5 представлен график функции d(t) и d(t-t).

 

 

 

 

 

 

 

 

 

 

 

 


Отметим некоторые свойства d-функции:

1.                                                                           (1.9).

Это следует из того, что  только при t=t.

2.                       (1.10).

В интеграле бесконечные пределы можно заменить конечными, но так, чтобы аргумент функции d(t-t) обращался в нуль внутри этих пределов.

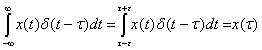                                                      (1.11).

3.     Преобразование Лапласа d-функции

                                     (1.12).

В частности, при t=0

                                                                                                     (1.13).

4.     Преобразование Фурье d-функции. При p=jv из 1.13 получим

                                                     (1.14)

При t=0

                                                                                                     (1.15),

т.е. спектр d-функции равен 1.

            Аналоговый сигнал f(t) называется периодическим если существует действительное число T, такое, что f(t+T)=f(t) для любых t. При этом T называется периодом сигнала. Примером периодического сигнала может служить сигнал, представленный на рис.1.2а, причем T=1/f. Другим примером периодического сигнала может служить последовательность d-функций, описываемая уравнением

                                                                                      (1.16)

график которой представлен на рис.1.6.

 

 

 

 

 

 

 

 

 

 

 

 

 


Дискретные сигналы отличаются от аналоговых тем, что их значения известны лишь в дискретные моменты времени. Дискретные сигналы описываются решетчатыми функциями – последовательностями – xд(nT), где T =const – интервал (период) дискретизации, n=0,1,2,…. Сама функция xд(nT) может в дискретные моменты принимать произвольные значения на некотором интервале. Эти значения функции называются выборками или отсчетами функции. Другим обозначением решетчатой функции x(nT) является x(n) или xn. На рис. 1.7а и 1.7б представлены примеры решетчатых функций  и . Последовательность x(n) может быть конечной или бесконечной, в зависимости от интервала определения функции.

 

 

 

 

 

 

 

 

 

 

 


Процесс преобразования аналогового сигнала в дискретный называется временная дискретизация. Математически процесс временной дискретизации можно описать как модуляцию входным аналоговым сигналом последовательности d-функций dT(t)

                                                                             (1.17)

Процесс восстановления аналогового сигнала из дискретного называется временная экстраполяция.

            Для дискретных последовательностей также вводятся понятия энергии и мощности. Энергией последовательности x(n) называется величина

                                                ,                                                (1.18)

Мощностью последовательности x(n) называется величина

                                                ,                             (1.19)

Для дискретных последовательностей сохраняются те же закономерности, касающиеся ограничения мощности и энергии, что и для непрерывных сигналов.

Периодической называют последовательность x(nT), удовлетворяющую условию x(nT)=x(nT+mNT), где m и N – целые числа. При этом N называют периодом последовательности. Периодическую последовательность достаточно задать на интервале периода, например при .

            Цифровые сигналы представляют собой дискретные сигналы, которые в дискретные моменты времени могут принимать лишь конечный ряд дискретных значений – уровней квантования. Процесс преобразования дискретного сигнала в цифровой называется квантованием по уровню. Цифровые сигналы описываются квантованными решетчатыми функциями xц(nT). Примеры цифровых сигналов представлены на рис. 1.8а и 1.8б.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


Связь между решетчатой функцией xд(nT) и квантованной решетчатой функцией xц(nT) определяется нелинейной функцией квантования xц(nT)=Fk(xд(nT)). Каждый из уровней квантования кодируется числом. Обычно для эих целей используется двоичное кодирование, так, что квантованные отсчеты xц(nT) кодируются двоичными числами с n разрядами. Число уровней квантования N и наименьшее число двоичных разрядов m, с помощью которых можно закодировать все эти уровни, связаны соотношением

,                                                         (1.20)

где int(x) – наименьшее целое число, не меньшее x.

Т.о., квантование дискретных сигналов состоит в представлении отсчета сигнала xд(nT) с помощью двоичного числа, содержащего m разрядов. В результате квантования отсчет представляется с ошибкой, которая называется ошибкой квантования

                                    .                                                 (1.21)

Шаг квантования Q определяется весом младшего двоичного разряда результирующего числа

                                    .                                                         (1.22)

            Основными способами квантования являются усечение и округление.

Усечение до m-разрядного двоичного числа состоит в отбрасывании всех младших разрядов числа кроме n старших. При этом ошибка усечения . Для положительных чисел при  любом способе кодирования . Для отрицательных чисел при использовании прямого кода ошибка усечения неотрицательна , а при использовании дополнительного кода эта ошибка неположительна . Таким образом, во всех случаях абсолютнок значение ошибки усечения не превосходит шага квантования:

                                    .                                        (1.23) 

График функции усечения дополнительного кода представлен на рис.1.9, а прямого кода – на рис.1.10.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


Округление отличается от усечения тем, что кроме отбрасывания младших разрядов числа модифицируется и m-й (младший неотбрасываемый) разряд числа. Его модификация заключается в том, что он либо остается неизменным или увеличивается на единицу в зависимости от того, больше или меньше отбрасываемая часть числа величины . Округление можно практически выполнить путем прибавления единицы к (m+1) – муразряду числа с последующим усечением полученного числа до n разрядов. Ошибка округления при всех способах кодирования лежит в пределах  и, следовательно,

                                    .                               (1.24)

График функции округления представлен на рис. 1.11.

 

 

 


           

 

 

 

 

 

 

 

 

 

 

 

 

Рассмотрение и использование различных сигналов предполагает возможность измерения значения этих сигналов в заданные моменты времени. Естественно возникает вопрос о достоверности (или наоборот, неопределенности) измерения значения сигналов. Этими вопросами занимается теория информации, основоположником которой является К.Шеннон. Основная идея теории информации состоит в том, что с информацией можно обращаться почти также, как с такими физическими величинами как масса и энергия.

            Точность измерений мы обычно характеризуем числовыми значениями полученных при измерении или предполагаемых погрешностей. При этом используются понятия абсолютной и относительной погрешностей. Если измерительное устройство имеет диапазон измерения от x1 до x2, с абсолютной погрешностью   ±D, не зависящей от текущего значения x измеряемой величины, то получив результат измерения в виде xn мы записываем его как xn±D и характеризуем относительной погрешностью .

            Рассмотрение этих же самых действий с позиции теории информации носит несколько иной характер, отличающийся тем, что всем перечисленным понятиям придается вероятностный, статистический смысл, а итог проведенного измерения истолковывается как сокращение области неопределенности измеряемой величины. В теории информации тот факт, что измерительный прибор имеет диапазон измерения от x1 до x2 означает, что при использовании этого прибора могут бытьполучены показания только в пределах от x1 до x2. Другими словами, вероятность получения отсчетов, меньших x1 или больших x2, равна 0. Вероятность же получения отсчетв где-то в пределах от x1 до x2 равна 1.

            Если предположить, что все результаты измерения в пределах от x1 до x2 равновероятны, т.е. плотность распределения вероятности для различных значений измеряемой величины вдоль всей шкалы прибора одинакова, то с точки зрения теории информации наше знание о значении измеряемой величины до измерения может быть представлено графиком распределения плотности вероятности p(x).

 

 

 

Поскольку полная вероятность получить отсчет где-то в пределах от x1 до x2 равна 1, то под кривой должна быть заключена площадь, равная 1, а это значит, что

                                                                                               (1.25).

            После проведения измерения получаем показание прибора, равное xn. Однако, вследствие погрешности прибора, равной ±D, мы не можем утверждать, что измеряемая величина точно равна xn. Поэтому мы записывает результат в виде xn±D. Это означает, что действительное значение измеряемой величины x лежит где-то в пределах от xn-D до xn+D. С точки зрения теории информации результат нашего измерения состоит лишь в том, что область неопределенности сократилась до величины 2D и характеризуется намного большей плотностью ве5роятности

                                                                                                      (1.26).

            Получение каой-либо информации об интересующей нас величине заключается, таким образом, в уменьшении неопределенности ее значения.

            В качестве характеристики неопределенности значения некоторой случайной величины К.Шеннон ввел понятие энтропии величины x, которая вычисляется как

                                                                            (1.27).

            Единицы измерения энтропии зависят от выбора основания логарифма в приведенных выражениях. При использовании десятичных логарифмов энтропия измеряется в т.н. десятичных единицах или дитах. В случае же использования двоичных логарифмов энтропия выражается в двоичных единицах или битах.

            В большинстве случаев неопределенность знания о значении сигнала определяется действием помех или шумов. Дезинформационное действие шума при передаче сигнала определяется энтропией шума как случайной величины. Если шум в вероятностном смысле не зависит от передаваемого сигнала, то независимо от статистики сигнала шуму можно приписывать определенную величину энтропии, которая и характеризует его дезинформационное действие. При этом анализ системы можно проводить раздельно для шума и сигнала, что резко упрощает решение этой задачи.

            Теорема Шеннона о количестве информации. Если на вход канала передачи информации подается сигнал с энтропией H(x), а шум в канале имеет энтропию H(D), то количество информации на выходе канала определяется как

                                                                                           (1.28).

            Если кроме основного канала передачи сигнала имеется дополнительный канал, то для исправления ошибок, возникших от шума с энтропией H(D), по этому каналу необходтмо передать дополнительное количество информации, не меньшее чем

                                                                                                     (1.29).

Эти данные можно так закодировать, что будет возможно скорректировать все ошибки, вызванные шумом, за исключением произвольно малой доли этих ошибок.

В нашем случае, для равномерно распределенной случайной величины, энтропия определяется как

                                          (1.30),

а оставшаяся или условная энтропия результата измерения после получения отсчета xn равна

                                                     (1.31).

Отсюда полученное количество информации равное разности исходной и оставшейся энтропии равно

                                            (1.32).

При анализе систем с цифровыми сигналами ошибки квантования рассматриваются как стационарный случайный процесс с равномерным распределением вероятности по диапазону распределения ошибки квантования. На рис. 1.12а, б и в приведены плотности вероятности ошибки квантования при округлении дополнительного кода, прямого кода и усечении соответственно.

 

 

 

 

 

 

 

 

 

 

 

 

 


Очевидно, что квантование является нелинейной операцией. Однако, при анализе используется линейная модель квантования сигналов, представленная на рис. 1.13.

Рис.1.13.
 
 

 

 

 

 

 

 


где f(nT) – дискретный сигнал, x(nT) – квантованный m – разрядный цифровой сигнал, e(nT) – ошибка квантования.

            Вероятностные оценки ошибок квантования делаются с помощью вычисления математического ожидания

                                               (1.33)

и дисперсии

                                                                  (1.34),

 

где pe – плотность вероятности ошибки. Для случаев округления и усечения будем иметь

 

            (1.35),

 

(1.36).

           

Временная дискретизация и квантование по уровню сигналов являются неотъемлемыми особенностями всех микропроцессорных систем управления, определяемыми ограниченным быстродействием и конечной разрядностью используемых микропроцессоров.